题目内容
4.已知O是△ABC的外接圆圆心,$|\overrightarrow{AB}|=4$,D是BC中点,若$\overrightarrow{AO}•\overrightarrow{AD}=5$,则$|\overrightarrow{AC}|$=2.分析 根据圆的知识与数量积的定义得出与已知条件相关的式子$\overrightarrow{AO}•\overrightarrow{AB}=\frac{1}{2}|\overrightarrow{AB}{|^2}=8$,$\overrightarrow{AO}•\overrightarrow{AC}=\frac{1}{2}|\overrightarrow{AC}{|^2}$,
再运用向量的加法的几何意义得出$\overrightarrow{AD}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$,代入$\overrightarrow{AO}•\overrightarrow{AD}=5$,展开即可.
解答 解:∵AB=4,O是△ABC的外接圆圆心,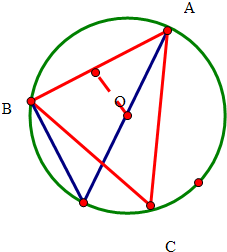
∴根据数量积意义$\overrightarrow{AO}•\overrightarrow{AB}=\frac{1}{2}|\overrightarrow{AB}{|^2}=8$,
同理$\overrightarrow{AO}•\overrightarrow{AC}=\frac{1}{2}|\overrightarrow{AC}{|^2}$,
∵D是BC中点,
∴$\overrightarrow{AD}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$,
∴$\overrightarrow{AO}•\overrightarrow{AD}=\frac{1}{2}(\overrightarrow{AO}•\overrightarrow{AB}+\overrightarrow{AO}•\overrightarrow{AC})$,
即$5=\frac{1}{2}×(8+\frac{1}{2}|\overrightarrow{AC}{|^2})$,
∴$|\overrightarrow{AC}|=2$.
故答案为:2.
点评 本题综合考查了向量的运算,数量积,结合几何图形,利用圆的知识与数量积的定义得出与已知条件相关的式子,整体运用,思维难度较大,题目很新颖.

 名校课堂系列答案
名校课堂系列答案
| A. | i>5 | B. | i≥5 | C. | i>6 | D. | i≥6 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |

| A. | 7 | B. | $\frac{15}{2}$ | C. | $\frac{23}{3}$ | D. | $\frac{47}{6}$ |