题目内容
9.设复数z≠-1,则“|z|=1”是“$\frac{z-1}{z+1}$是纯虚数”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
分析 根据充分条件和必要条件的定义结合复数的有关概念进行判断即可.
解答 解:若$\frac{z-1}{z+1}$是纯虚数纯虚数,
则设$\frac{z-1}{z+1}$=bi,(b≠0),z=x+yi,
则z-1=bi(z+1),
即x-1+yi=bi(x+1+yi)=-by+(x+1)bi,
则$\left\{\begin{array}{l}{x-1=-by}\\{(x+1)b=y}\end{array}\right.$,两式相除消去b得(x-1)(x+1)=-y2,
即x2+y2=1,此时|z|=1,即必要性成立,
若z=1,满足|z|=1,但此时$\frac{z-1}{z+1}$=0,不是纯虚数,故充分性不成立,
故“|z|=1”是“$\frac{z-1}{z+1}$是纯虚数”的必要不充分条件,
故选:B
点评 本题主要考查复数的有关概念以及充分条件和必要条件的判断,利用复数的四则运算进行化简是解决本题的关键.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
18.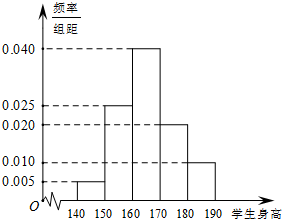 为调查学生身高的情况,随机抽测了高三两个班120名学生的身高(单位:cm),所得数据均在区间[140,190]上,其频率分布直方图如图所示(左下),则在抽测的120名学生中,身高位于区间[160,180)上的人数为( )
为调查学生身高的情况,随机抽测了高三两个班120名学生的身高(单位:cm),所得数据均在区间[140,190]上,其频率分布直方图如图所示(左下),则在抽测的120名学生中,身高位于区间[160,180)上的人数为( )
 为调查学生身高的情况,随机抽测了高三两个班120名学生的身高(单位:cm),所得数据均在区间[140,190]上,其频率分布直方图如图所示(左下),则在抽测的120名学生中,身高位于区间[160,180)上的人数为( )
为调查学生身高的情况,随机抽测了高三两个班120名学生的身高(单位:cm),所得数据均在区间[140,190]上,其频率分布直方图如图所示(左下),则在抽测的120名学生中,身高位于区间[160,180)上的人数为( )| A. | 70 | B. | 71 | C. | 72 | D. | 73 |
19.在△ABC中,角A,B,C所对的边长为a,b,c,若a=$\sqrt{2}$,b=2,sinB+cosB=$\sqrt{2}$,则A=( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{2π}{3}$ |