题目内容
14.已知函数f(x)=|x+1|+2|x-1|-a(1)若a=1,求不等式f(x)>x+2的解集
(2)若不等式f(x)≤a(x+2)的解集为非空集合,求a的取值范围.
分析 (1)把要解的不等式等价转化为与之等价的三个不等式组,求出每个不等式组的解集,再取并集,即得所求.
(2)由题意可得|x+1|+2|x-1|≤a(x+3)能成立.设g(x)=|x+1|+2|x-1|,由题意可得f(x)的图象有一部分位于直线线y=a(x+3)的下方.求得PA、BC的斜率,数形结合求得a的范围.
解答 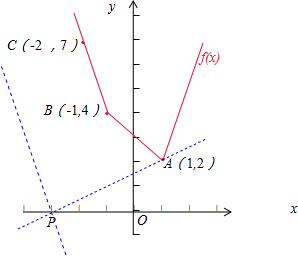 解:(1)当a=1时,f(x)=|x+1|+2|x-1|-1,不等式f(x)>x+2,即|x+1|+2|x-1|>x+3.
解:(1)当a=1时,f(x)=|x+1|+2|x-1|-1,不等式f(x)>x+2,即|x+1|+2|x-1|>x+3.
∴$\left\{\begin{array}{l}{x<-1}\\{1-3x>x+3}\end{array}\right.$①或$\left\{\begin{array}{l}{-1≤x<1}\\{3-x>x+3}\end{array}\right.$②或$\left\{\begin{array}{l}{x≥1}\\{3x-1>x+3}\end{array}\right.$③.
解①求得x<-1,解②求得-1≤x<0,解③求得x>2,
综上可得,原不等式的解集为{x|x<0,或x>2}.
(2)由题意可得f(x)≤a(x+2)有解,化简f(x)≤a(x+2)可得|x+1|+2|x-1|≤a(x+3).
设g(x)=|x+1|+2|x-1|=$\left\{\begin{array}{l}{1-3x,x<-1}\\{3-x,-1≤x<1}\\{3x-1,x≥1}\end{array}\right.$,由于直线y=a(x+3)经过定点P(-3,0),如图:
由题意可得f(x)的图象有一部分位于直线线y=a(x+3)的下方.
由于PA的斜率KPA=$\frac{2-0}{1+3}$=$\frac{1}{2}$,直线BC的斜率 KBC=-3,
故a的范围为(-∞,-3)∪($\frac{1}{2}$,+∞).
点评 本题主要考查绝对值不等式的解法,函数的能成立问题,体现了转化、分类讨论、数形结合的数学思想,属于中档题.

 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案| A. | $\frac{5}{3}$ | B. | $\frac{5}{4}$ | C. | $\frac{4}{3}$ | D. | $\frac{5}{2}$ |

| A. | 21 | B. | 37 | C. | 57 | D. | 62 |
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{2π}{3}$ |
| A. | $\frac{{9-4\sqrt{2}}}{7}$ | B. | $\frac{{2-\sqrt{2}}}{7}$ | C. | $\frac{{9+4\sqrt{2}}}{7}$ | D. | $\frac{{2+\sqrt{2}}}{7}$ |
 如图,网格纸上小正方形的边长为1,若粗线画出的是某几何体的三视图,则此几何体的体积为( )
如图,网格纸上小正方形的边长为1,若粗线画出的是某几何体的三视图,则此几何体的体积为( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |