题目内容
13.已知数列{an}是公差d>0的等差数列,且a2+a3=7,a2•a3=12,数列{bn}是等比数列,公比q=b1=$\frac{4}{9}$a1.(1)求数列{an}和数列{bn}的通项公式;
(2)设cn=an•bn,试判断数列{cn}是否有最大值;若有最大值,则求出第几项最大,最大值是多少?若没有,请说明理由.
分析 (1)利用等差数列与等比数列的通项公式即可得出;
(2)cn=an•bn=$(n+1)•(\frac{8}{9})^{n}$,作商可得:$\frac{{c}_{n+1}}{{c}_{n}}$=$\frac{n+2}{n+1}•\frac{8}{9}$,令$\frac{{c}_{n+1}}{{c}_{n}}≥1$,解得n≤7,即可得出数列的单调性,进而得出结论.
解答 解:(1)∵数列{an}是公差d>0的等差数列,且a2+a3=7,a2•a3=12,
∴a2=3,a3=4,d=4-3=1,
2a1+3×1=7,解得a1=2,
∴an=2+(n-1)=n+1.
∵数列{bn}是等比数列,公比q=b1=$\frac{4}{9}$a1=$\frac{8}{9}$.
∴${b}_{n}=(\frac{8}{9})^{n}$.
(2)cn=an•bn=$(n+1)•(\frac{8}{9})^{n}$,
$\frac{{c}_{n+1}}{{c}_{n}}$=$\frac{n+2}{n+1}•\frac{8}{9}$,
令$\frac{{c}_{n+1}}{{c}_{n}}≥1$,解得n≤7,
∴数列c1<c2<…<c7=c8>c9>….
∴当n=7或8时,数列{cn}有最大值,c7=c8=$\frac{{8}^{8}}{{9}^{7}}$.
点评 本题考查了等差数列的通项公式、数列的单调性,考查了分类讨论的思想方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
18.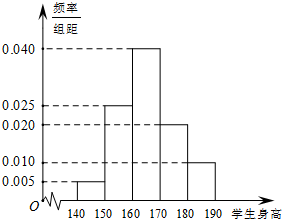 为调查学生身高的情况,随机抽测了高三两个班120名学生的身高(单位:cm),所得数据均在区间[140,190]上,其频率分布直方图如图所示(左下),则在抽测的120名学生中,身高位于区间[160,180)上的人数为( )
为调查学生身高的情况,随机抽测了高三两个班120名学生的身高(单位:cm),所得数据均在区间[140,190]上,其频率分布直方图如图所示(左下),则在抽测的120名学生中,身高位于区间[160,180)上的人数为( )
 为调查学生身高的情况,随机抽测了高三两个班120名学生的身高(单位:cm),所得数据均在区间[140,190]上,其频率分布直方图如图所示(左下),则在抽测的120名学生中,身高位于区间[160,180)上的人数为( )
为调查学生身高的情况,随机抽测了高三两个班120名学生的身高(单位:cm),所得数据均在区间[140,190]上,其频率分布直方图如图所示(左下),则在抽测的120名学生中,身高位于区间[160,180)上的人数为( )| A. | 70 | B. | 71 | C. | 72 | D. | 73 |
5.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)与抛物线y2=2px(p>0)有相同的焦点,且双曲线的一条渐近线与抛物线的准线交于点$(-5,-\frac{15}{4})$,则双曲线的离心率为( )
| A. | $\frac{5}{3}$ | B. | $\frac{5}{4}$ | C. | $\frac{4}{3}$ | D. | $\frac{5}{2}$ |
3. 如图,网格纸上小正方形的边长为1,若粗线画出的是某几何体的三视图,则此几何体的体积为( )
如图,网格纸上小正方形的边长为1,若粗线画出的是某几何体的三视图,则此几何体的体积为( )
 如图,网格纸上小正方形的边长为1,若粗线画出的是某几何体的三视图,则此几何体的体积为( )
如图,网格纸上小正方形的边长为1,若粗线画出的是某几何体的三视图,则此几何体的体积为( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |