题目内容
7.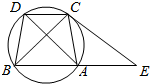 如图,已知圆中$\widehat{AC}$=$\widehat{BD}$,AC=CD,过C点的圆的切线与BA的延长线交于E点.
如图,已知圆中$\widehat{AC}$=$\widehat{BD}$,AC=CD,过C点的圆的切线与BA的延长线交于E点.证明:(1)AD∥CE
(2)CD.CE=BC.AC.
分析 (1)证明∠ACE=∠DAC,即可证明AD∥CE
(2)证明△DCA∽△BCE,可得$\frac{DC}{BC}=\frac{AC}{CE}$,即可证明CD•CE=BC•AC.
解答 证明:(1)因为EC与圆相切于点C,
故∠ACE=∠ABC=∠ADC
因为AC=CD,
所以∠DAC=∠ADC.
所以∠ACE=∠DAC.
所以AD∥CE
(2)因为$\widehat{AC}$=$\widehat{BD}$,AC=CD,
所以∠DAB=∠DAC
因为∠DAB=∠CEA,
所以∠CEA=∠DAC,
因为∠CDA=∠CBA,
所以△DCA∽△BCE,
所以$\frac{DC}{BC}=\frac{AC}{CE}$
所以CD•CE=BC•AC.
点评 本题主要考查圆的切线的判定定理的证明、弦切角的应用、三角形相似等基础知识,考查运化归与转化思想.属于中档题.

练习册系列答案
相关题目
15.已知函数f(x)=$\left\{\begin{array}{l}{{e}^{x},x<0}\\{x+m,x≥0}\end{array}\right.$,以下说法正确的是( )
| A. | ?m∈R,函数f(x)在定义域上单调递增 | B. | ?m∈R,函数f(x)存在零点 | ||
| C. | ?m∈R,函数f(x)有最大值 | D. | ?m∈R,函数f(x)没有最小值 |
19.某中学采用系统抽样方法,从该校高一年级全体500名学生中抽50名学生做牙齿健康检查.现将500名学生从1到500进行编号.已知从21~30这10个数中取的数是24,则在第1小组1~10中随机抽到的数是( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
17.P是边长为a的正三角ABC所在平面外一点,PA=PB=PC=a,E、F是AB和PC的中点,则异面直线PA与EF所成的角为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
 如图所示,四边形ABCD是正方形,PA⊥平面ABCD,且PA=AB.
如图所示,四边形ABCD是正方形,PA⊥平面ABCD,且PA=AB. 如图,AB是圆O的直径,AC是弦,∠BAC的平分线AD交圆O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.
如图,AB是圆O的直径,AC是弦,∠BAC的平分线AD交圆O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.