题目内容
2.定义在非零实数集上的函数f(x)对任意非零实数x,y满足:f(xy)=f(x)+f(y),且当0<x<1时,f(x)<0.(Ⅰ)求f(-1)及f(1)的值;
(Ⅱ)求证:f(x)是偶函数;
(Ⅲ)解不等式:f(2)+f(x2-$\frac{1}{2}$)≤0.
分析 (Ⅰ)分别令x=y=1,x=y=-1,求出f(1)和f(-1)的值;
(Ⅱ)令x=x,y=-1,即可求出f(-x)=f(x),f(x)为偶函数
(Ⅲ)先判断函数的单调性,在根据单调性得到关于x的不等式组,解得即可.
解答 解:(Ⅰ)令x=y=1,
则f(1)=f(1)+f(1),
∴f(1)=0,
再令x=y=-1,
则f(1)=f(-1)+f(-1),
∴f(-1)=0,
(Ⅱ)令x=x,y=-1,
则f(-x)=f(x)+f(-1)=f(x),
∴f(-x)=f(x),
∴f(x)为偶函数;
(Ⅲ)任取x1,x2∈(0,+∞),且x1<x2,
∴$\frac{{x}_{1}}{{x}_{2}}$<1,
∴f($\frac{{x}_{1}}{{x}_{2}}$)<0,
∴f(x1)=f(x2•$\frac{{x}_{1}}{{x}_{2}}$)=f(x2)+f($\frac{{x}_{1}}{{x}_{2}}$)<f(x2),
∴f(x)在(0,+∞)是增函数,
∴f(x)在(-∞,0)是减函数,
∵f(2)+f(x2-$\frac{1}{2}$)=f(2x2-1)≤0=f(1)=f(-1),
∴$\left\{\begin{array}{l}{2{x}^{2}-1<0}\\{2{x}^{2}-1≥-1}\end{array}\right.$或$\left\{\begin{array}{l}{2{x}^{2}-1>0}\\{2{x}^{2}-1≤1}\end{array}\right.$,
解得-$\frac{\sqrt{2}}{2}$<x<$\frac{\sqrt{2}}{2}$.或-1≤x<-$\frac{\sqrt{2}}{2}$,或$\frac{\sqrt{2}}{2}$<x≤1,
∴不等式的解集为[-1,-$\frac{\sqrt{2}}{2}$)∪(-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$)∪($\frac{\sqrt{2}}{2}$,1]
点评 本题考查了函数的奇偶性及单调性的证明与应用,同时考查了恒成立问题的应用,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图,在直四棱柱ABCD-A1B1C1D1中,点E,F分别在AA1,CC1上,且AE=$\frac{4}{5}$AA1,CF=$\frac{1}{3}$CC1,点A,C到BD的距离之比为2:3,则三棱锥E-BCD和F-ABD的体积比$\frac{{V}_{E-BCD}}{{V}_{F-ABD}}$=$\frac{18}{5}$.
如图,在直四棱柱ABCD-A1B1C1D1中,点E,F分别在AA1,CC1上,且AE=$\frac{4}{5}$AA1,CF=$\frac{1}{3}$CC1,点A,C到BD的距离之比为2:3,则三棱锥E-BCD和F-ABD的体积比$\frac{{V}_{E-BCD}}{{V}_{F-ABD}}$=$\frac{18}{5}$. 如图所示,在三棱柱ABC-A1B1C1中,∠ACB=90°,AA1⊥平面ABC,AC=BC=CC1,M,N分别为A1B,B1C1的中点.
如图所示,在三棱柱ABC-A1B1C1中,∠ACB=90°,AA1⊥平面ABC,AC=BC=CC1,M,N分别为A1B,B1C1的中点.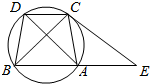 如图,已知圆中$\widehat{AC}$=$\widehat{BD}$,AC=CD,过C点的圆的切线与BA的延长线交于E点.
如图,已知圆中$\widehat{AC}$=$\widehat{BD}$,AC=CD,过C点的圆的切线与BA的延长线交于E点. 如图,四棱锥F-ABCD的底面ABCD是菱形,其对角线AC=2,BD=$\sqrt{2}$.CF与平面 ABCD垂直,CF=2.求二面角B-AF-D的大小.
如图,四棱锥F-ABCD的底面ABCD是菱形,其对角线AC=2,BD=$\sqrt{2}$.CF与平面 ABCD垂直,CF=2.求二面角B-AF-D的大小.