题目内容
甲、乙两名同学参加一项射击游戏，两人约定，其中任何一人每射击一次，击中目标得2分，未击中目标得0分．若甲、乙两名同学射击的命中率分别为
和p，且甲、乙两人各射击一次所得分数之和为2的概率为
，假设甲、乙两人射击互不影响
（1）求p的值；
（2）记甲、乙两人各射击一次所得分数之和为ξ，求ξ的分布列和数学期望．
| 3 |
| 5 |
| 9 |
| 20 |
（1）求p的值；
（2）记甲、乙两人各射击一次所得分数之和为ξ，求ξ的分布列和数学期望．
（1）设“甲射击一次，击中目标”为事件A，
“乙射击一次，击中目标”为事件B，
“甲射击一次，未击中目标”为事件
，
“乙射击一次，未击中目标”为事件
，
则P（A）=
，P（
）=
，P（B）=P，P（
）=1-P
依题意得：
(1-P)+
P=
，
解得P=
，
故p的值为
．
（2）ξ的取值分别为0，2，4．
P（ξ=0）=P（
）=P（
）P（
）=
×
=
，
P（ξ=2）=
P（ξ=4）=P（AB）=P（A）P（B）=
×
=
，
∴ξ的分布列为
∴Eξ=0×
+2×
+4×
=
“乙射击一次，击中目标”为事件B，
“甲射击一次，未击中目标”为事件
| . |
| A |
“乙射击一次，未击中目标”为事件
| . |
| B |
则P（A）=
| 3 |
| 5 |
| . |
| A |
| 2 |
| 5 |
| . |
| B |
依题意得：
| 3 |
| 5 |
| 2 |
| 5 |
| 9 |
| 20 |
解得P=
| 3 |
| 4 |
故p的值为
| 3 |
| 4 |
（2）ξ的取值分别为0，2，4．
P（ξ=0）=P（
| . |
| A |
| . |
| B |
| . |
| A |
| . |
| B |
| 2 |
| 5 |
| 1 |
| 4 |
| 1 |
| 10 |
P（ξ=2）=
| 9 |
| 20 |
P（ξ=4）=P（AB）=P（A）P（B）=
| 3 |
| 5 |
| 3 |
| 4 |
| 9 |
| 20 |
∴ξ的分布列为
∴Eξ=0×
| 1 |
| 10 |
| 9 |
| 20 |
| 9 |
| 20 |
| 27 |
| 10 |
练习册系列答案
相关题目
分别写在大小、形状都相同的
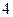张卡片上，将它们反扣后（数字向下），再从左到右随机的依次摆放，然后从左到右依次翻卡片：若第一次就翻出数字
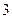则停止翻卡片；否则就继续翻，若将翻出的卡片上的数字依次相加所得的和是
，求出
表示抽取的3名工人中男工人数，求