Question

【题目】如图所示，在三棱锥中，，且，，分别是，的中点．则异面直线与所成角的余弦值为___________.

Answer 1

【答案】

【解析】

以S为原点，SA，SB，SC为x，y，z轴，建立空间直角坐标系，利用向量法能求出异面直线SM与BN所成角的余弦值．

∵在三棱锥S﹣ABC中，SA＝SC＝2SB，且∠ASB＝∠BSC＝∠CSA，

M，N分别是AB，SC的中点．

∴以S为原点，SA，SB，SC为x，y，z轴，建立空间直角坐标系，

设SA＝SC＝2SB＝2，

则S（0，0，0），N（0，0，1），A（2，0，0），B（0，1，0），M（1，，0），

（1，，0），（0，﹣1，1），

设异面直线SM与BN所成角为θ，

则cosθ．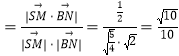

∴异面直线SM与BN所成角的余弦值为．

故答案为：．