题目内容
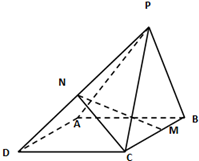
一个四棱锥P一ABCD的正视图是边长为2的正方形及其一条对角线,侧视图和俯视图全全等的等腰直角三角形,直角边长为2,直观图如图.
(1)求四棱锥P一ABCD的体积:
(2)求二面角C-PB-A大小;
(3)M为棱PB上的点,当PM长为何值时,CM⊥PA?
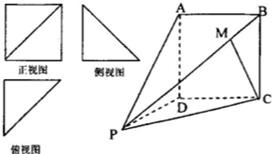
(1)由三视图可知,PD⊥平面ABCD,
∴
四棱锥P-ABCD的体积V=SABCD•PD=;
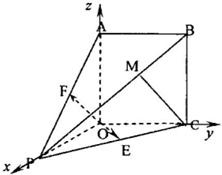
(2)如图,以D为坐标原点,分别以DP、DC、DA所在
直线为x轴、y轴、z轴建立空间直角坐标系.设CP中
点为E,则
OE⊥PC,OE⊥BC,所以是平面PBC的法向量;设AP中点为F,同理
可知
是平面PAB的法向量.
知
是平面PAB的法向量.
=(1,1,0),=(1,0,1),
设二面角
C-PB-A的平面角为θ,则|cosθ|=|=,显然
θ>,
所以二面角C-PB-A大小为
;
(3)P(2,0,0),B(0,2,2),C(0,2,0),A(0,0,2),∵PMB共线,
∴可设
=k•=(-2k,2k,2k),k∈R,=+=(2-2k,-2+2k,2k),
=(-2,0,2),
∵
CM⊥PA,所以•
=8k-4=0,∴
k=∴
=(-1,1,1),||=∴PM的长为
时,CM⊥PA
练习册系列答案
相关题目