Question

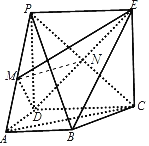
【题目】如图，四边形PDCE为矩形，四边形ABCD为梯形，平面PDCE⊥平面ABCD，∠BAD＝∠ADC＝90°，，，若M为PA的中点，PC与DE交于点N.

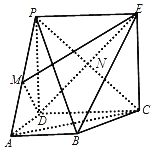
（1）求证：AC∥面MDE；

（2）求证：PE⊥MD；

（3）求点N到平面ABM的距离.

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）

【解析】

（1）根据三角形中位线性质得线线平行，再根据线面平行判定定理得结果；

（2）先根据面面垂直性质定理得AD⊥平面PDCE，再根据线面垂直判断与性质定理证结果；

（3）利用等体积法，即由VP﹣ABC＝VC﹣PAB求点面距.

（1）证明：连接MN，∵四边形PDCE为矩形，PC与DE交于点N，∴N为PC的中点，

又M为PA的中点，∴MN∥AC，

而MN平面MDE，AC平面MDE，

∴AC∥面MDE；

（2）证明：∵平面PDCE⊥平面ABCD，平面PDCE∩平面ABCD＝CD，∠ADC＝90°，

∴AD⊥平面PDCE，则AD⊥PE，又PE⊥PD，PD∩AD＝D，

∴PE⊥平面PAD，

则PE⊥MD；

（3）解：∵，，

∴PA＝，则，，

设C到平面PAB的距离为h，则由VP﹣ABC＝VC﹣PAB，

得，解得h＝，

∵N为PC的中点，∴点N到平面ABM的距离为.