题目内容
关于直线a、b、l及平面M、N,下列命题中正确的是( )
A若a∥M,b∥M,则a∥b
B若a∥M,b⊥a,则b⊥M
C若a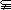 M,b
M,b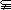 M,且l⊥a,l⊥b,则l⊥M
M,且l⊥a,l⊥b,则l⊥M
D若a⊥M,M∥N,则a⊥N
A若a∥M,b∥M,则a∥b
B若a∥M,b⊥a,则b⊥M
C若a
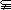 M,b
M,b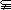 M,且l⊥a,l⊥b,则l⊥M
M,且l⊥a,l⊥b,则l⊥MD若a⊥M,M∥N,则a⊥N
D
试题分析:
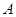 选项不正确,平行于同一个平面的两条直线可能相交,平行,异面.
选项不正确,平行于同一个平面的两条直线可能相交,平行,异面.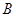 选项不正确,垂直于一个平面的平行线的直线与该平面的关系可以是平行,相交,或在面内;
选项不正确,垂直于一个平面的平行线的直线与该平面的关系可以是平行,相交,或在面内;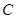 选项不正确,由线面垂直的判定定理知,本命题中缺少两线相交的条件,故不能依据线面垂直的判定定理得出线面垂直.
选项不正确,由线面垂直的判定定理知,本命题中缺少两线相交的条件,故不能依据线面垂直的判定定理得出线面垂直. 选项正确,由
选项正确,由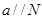 知可在面
知可在面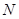 内找到一条直线与
内找到一条直线与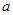 平行,且可以由
平行,且可以由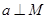 证得这条线与
证得这条线与 垂直,如此则可得出面面垂直的判定定理成立的条件.
垂直,如此则可得出面面垂直的判定定理成立的条件.故选
 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
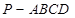 中,底面
中,底面 是直角梯形,
是直角梯形,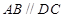 ,
,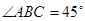 ,
,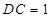 ,
,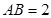 ,
,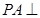 平面
平面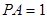 .
. 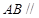 平面
平面 ;
; 平面
平面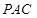 ;
;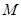 是
是 的中点,求三棱锥
的中点,求三棱锥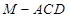 的体积.
的体积.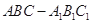 中,
中,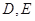 分别是
分别是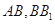 的中点,
的中点,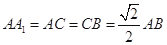 .
.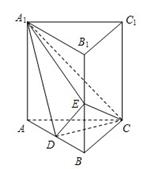
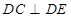 ;
;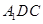 所成角的正弦值.
所成角的正弦值.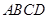 中,
中,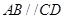 ,
,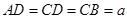 ,
,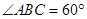 ,平面
,平面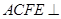 平面
平面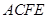 是矩形,
是矩形,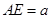 ,点
,点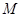 在线段EF上.
在线段EF上.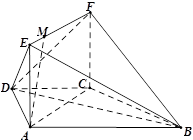
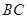 与
与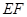 所成的角;
所成的角;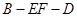 的余弦值.
的余弦值.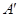 .
.
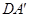 ⊥EF;
⊥EF;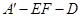 的平面角的余弦值.
的平面角的余弦值. ,M是DE的中点,F是AC的中点,且AC=4,
,M是DE的中点,F是AC的中点,且AC=4,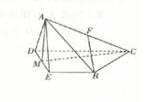
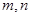 是两条不同的直线,
是两条不同的直线,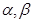 是两个不同的平面,则下列命题中的真命题是( )
是两个不同的平面,则下列命题中的真命题是( )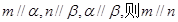
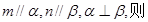
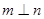
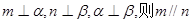
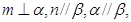 则
则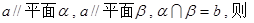
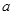 与
与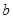 ( )
( )