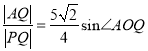题目内容
【题目】选修4-4：坐标系与参数方程
在极坐标系中，曲线的极坐标方程为
，以极点为原点，极轴为
轴的非负半轴建立平面直角坐标系，直线
的参数方程为
（
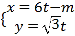为参数， 
）.
（1）求曲线
的直角坐标方程和直线
的普通方程；
（2）若曲线
上的动点
到直线
的最大距离为
，求
的值.
【答案】（1）
，直线
的普通方程为： 
（2）
【解析】试题分析：（1）因为
， 
，故可得曲线
，直线
的普通方程为： 
；（2）由点到直线的距离公式可得： 
， 
.
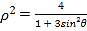
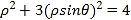试题解析：
（1）由
得
，
因为
， 
，故可得曲线
，
由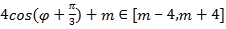
消去参数
可得直线
的普通方程为： 
；
（2）由（1）可得曲线
的参数方程为： 
（
为参数），
由点到直线的距离公式可得：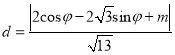 
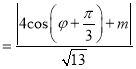
据条件可知
，由于
，分如下情况：
①
时，由
得
；
②
时，由
得
；
综上， 
.
【题目】某农科站技术员为了解某品种树苗的生长情况，在该批树苗中随机抽取一个容量为100的样本，测量树苗高度（单位：
）．经统计，高度在区间
内，将其按
，
，
，
，
，
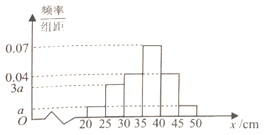
分成6组，制成如图所示的频率分布直方图，其中高度不低于
的树苗为优质树苗．
附：
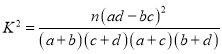，其中
|
|
|
|
|
|
|
|
|
|
（1）求频率分布直方图中
的值；
（2）已知所抽取的这100棵树苗来自于甲、乙两个地区，部分数据如下
列联表所示，将列联表补充完整，并根据列联表判断是否有
％的把握认为优质树苗与地区有关？
甲地区 | 乙地区 | 合计 | |
优质树苗 | 5 | ||
非优质树苗 | 25 | ||
合计 |
【题目】汽车是碳排放量比较大的行业之一，欧盟规定，从2015年开始，将对
排放量超过130g/km的
型新车进行惩罚（视为排放量超标），某检测单位对甲、乙两类型品牌抽取5辆进行排放量检测，记录如下（单位：g/km）：
甲 | 80 | 110 | 120 | 140 | 150 |
乙 | 100 | 120 | x | y | 160 |
经测算发现，乙品牌车排放量的平均值为
.
（Ⅰ）从被检测的5辆甲类品牌中任取2辆，则至少有一辆排放量超标的概率是多少?
（Ⅱ）若乙类品牌的车比甲类品牌的的排放量的稳定性要好，求x的范围.
