题目内容
【题目】已知椭圆
的短轴长为2，且椭圆
的离心率为
.
（1）求椭圆的方程；
（2）过椭圆的上焦点作相互垂直的弦
，
，求
为定值.
【答案】（1）
（2）
【解析】
（1）由题意得到b,a，即可得结果.
（2）通过分直线AB、CD中有一个斜率不存在与均存在两种情况讨论．当直线AB、CD中有一个斜率不存在时，通过计算可知|AB|＝
、|CD|＝
，进而可得结论；当直线AB、CD斜率均存在时，设直线AB方程为：y＝k（x
），则直线CD方程为：y
（x），通过联立直线与椭圆方程、利用韦达定理、两点间距离公式计算可知|AB|
，进而计算可得结论．
（1）由题意可知
，
.又椭圆
的离心率为
，则
，
故椭圆的方程为
（2）当直线
的斜率不存在或为零时，
当直线的斜率存在，且不为零时，设直线的方程为
，
，
，
联立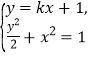
消去
，整理得
，
则
，
，
故
.
同理可得：
，
∴
练习册系列答案
相关题目
【题目】为保护农民种粮收益，促进粮食生产，确保国家粮食安全，调动广大农民粮食生产的积极性，从2004年开始，国家实施了对种粮农民直接补贴.通过对2014～2018年的数据进行调查，发现某地区发放粮食补贴额
（亿元）与该地区粮食产量
（万亿吨）之间存在着线性相关关系.统计数据如下表：
年份 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 |
补贴额 | 9 | 10 | 12 | 11 | 8 |
粮食产量 | 23 | 25 | 30 | 26 | 21 |
（1）请根据如表所给的数据，求出关于的线性回归直线方程
；
（2）通过对该地区粮食产量的分析研究，计划2019年在该地区发放粮食补贴额7亿元，请根据（1）中所得的线性回归直线方程，预测2019年该地区的粮食产量.
（参考公式：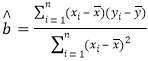
，
）
