Question

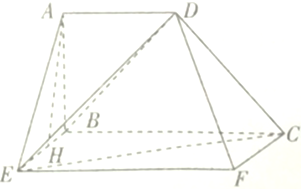
【题目】已知等腰梯形ABCD(如图1所示)，其中AB∥CD，E，F分别为AB和CD的中点，且AB＝EF＝2，CD＝6，M为BC中点．现将梯形ABCD沿着EF所在直线折起，使平面EFCB⊥平面EFDA(如图2所示)，N是线段CD上一动点，且.

(1)求证：MN∥平面EFDA；

(2)求三棱锥A－MNF的体积．

Answer 1

【答案】（1）见解析；（2）1

【解析】(1)证明：过点M作MP⊥EF于点P，过点N作NQ⊥FD于点Q，连接PQ.由题知，平面EFCB⊥平面EFDA，

又MP⊥EF，平面EFCB∩平面EFDA＝EF，

∴MP⊥平面EFDA.

又EF⊥CF，EF⊥DF，CF∩DF＝F，

∴EF⊥平面CFD.

又NQ平面CFD，∴NQ⊥EF.

又NQ⊥FD，EF∩FD＝F，

∴NQ⊥平面EFDA，

∴MP∥NQ.

又CN＝ND，∴NQ＝CF＝×3＝2，

且MP＝ (BE＋CF)＝×(1＋3)＝2，

∴MP綊NQ，∴四边形MNQP为平行四边形．

∴MN∥PQ.

又∵MN平面EFDA，PQ平面EFDA，

∴MN∥平面EFDA.

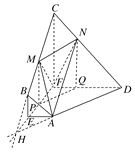
(2)延长DA，CB相交于一点H，则H∈CB，H∈DA.

又∵CB平面FEBC，DA平面FEAD.

∴H∈平面FEBC，H∈平面FEAD，

即H∈平面FEBC∩平面FEAD＝EF，

∴DA，FE，CB交于一点H，且HE＝EF＝1.

V三棱锥F－CDH＝V三棱锥C－HFD＝·S△HFD·CF＝，

又由平面几何知识得，则，

∴V三棱锥A－MNF＝V三棱锥F－AMN＝V三棱锥F－CDH＝＝1.