题目内容
【题目】如果函数![]() 满足
满足![]() 且
且![]() 是它的零点,则函数
是它的零点,则函数![]() 是“有趣的”,例如
是“有趣的”,例如![]() 就是“有趣的”,已知
就是“有趣的”,已知![]() 是“有趣的”.
是“有趣的”.
(1)求出b、c并求出函数![]() 的单调区间;
的单调区间;
(2)若对于任意正数x,都有![]() 恒成立,求参数k的取值范围.
恒成立,求参数k的取值范围.
【答案】(1)![]() ,
,![]() ,单减区间为0,1),单增区间为
,单减区间为0,1),单增区间为![]() ;(2)
;(2)![]()
【解析】
(1)根据定义得方程恒成立,解得b、c,再根据复合函数单调性确定函数![]() 的单调区间;
的单调区间;
(2)先化简不等式,再求导数,根据导函数符号分类讨论,利用导数证明![]() 恒成立,再说明
恒成立,再说明![]() 不恒成立.
不恒成立.
(1)因为![]() 是“有趣的”,所以
是“有趣的”,所以![]()
即![]()
![]()
![]()
![]() 的定义域为
的定义域为![]() ,单减区间为(0,1),单增区间为
,单减区间为(0,1),单增区间为![]() .
.
(2)参数![]() 的取值范围为
的取值范围为![]() .
.
引理:不等式![]() 对任意正数y都成立。证明如下:
对任意正数y都成立。证明如下:
![]()
由![]() 恒成立,得
恒成立,得![]() 恒成立。.
恒成立。.
我们构造函数![]() 。注意到
。注意到![]() 。
。

构造![]() ,注意到
,注意到![]() ,且
,且
![]()
我们以下分两部分进行说明:
第一部分:![]() 时,
时,![]() 恒成立。
恒成立。
![]() 时,由引理得:
时,由引理得:![]() ,知道
,知道![]() ,
,
从而当![]() 时有
时有![]() ,
,![]() 时有
时有![]() ,所以
,所以 在(0,1)上为负,在
在(0,1)上为负,在![]() 上为正。
上为正。
从而![]() 在
在![]() 上单减,在
上单减,在![]() 上单增,最小值为
上单增,最小值为![]() 。
。
从而![]()
第二部分:![]() 时,不满足条件。
时,不满足条件。
构造函数![]() 。
。
(ⅰ)若![]() ,则对于任意
,则对于任意![]() ,都有
,都有![]() 。
。
(ⅱ)若![]() ,则对于任意
,则对于任意![]() ,
,![]() ,
,
而 ,所以在(0,1)上
,所以在(0,1)上![]() 有唯一零点
有唯一零点![]() ,同时在
,同时在![]() ,时都有
,时都有![]() 。
。
于是只要![]() ,无论是(ⅰ)还是(ⅱ),我们总能找到一个实数
,无论是(ⅰ)还是(ⅱ),我们总能找到一个实数![]() ,在
,在![]() 时都有
时都有![]() 。
。
这样在 时,都有
时,都有![]() ,结合
,结合![]() ,所以
,所以 时
时![]() ,从而在
,从而在 时有
时有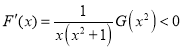 。
。![]() ,所以
,所以 时
时![]() ,不满足要求。
,不满足要求。

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目