题目内容
【题目】已知函数![]() .
.
(1)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若![]() ,
,![]() 时,
时,![]() 恒成立,求m的取值范围.
恒成立,求m的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)求出![]() ,求出切点处的导数值,即为切线的斜率,求出
,求出切点处的导数值,即为切线的斜率,求出![]() ,由直线的点斜式方程可求出切线的方程.
,由直线的点斜式方程可求出切线的方程.
(2)分为![]() 和
和![]() 两种情况进行讨论,
两种情况进行讨论,![]() ,运用导数求出当
,运用导数求出当![]() ,
,![]() ,
,![]() 三种情况下的
三种情况下的![]() 的最值,从而可求出参数的取值范围.
的最值,从而可求出参数的取值范围.
(1)由![]() ,得
,得![]() ,
,
所以![]() ,
,![]() .
.
所以曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,即
,即![]() .
.
(2)当![]() 时,
时,![]() ,则
,则![]() 时,
时,![]() 恒成立.
恒成立.
当![]() 时,
时,![]() ,
,![]() , 当
, 当![]() 时,
时,![]() 恒成立;
恒成立;
当![]() ,
,![]() 时,
时,![]() 恒成立等价于
恒成立等价于![]() .
.
令![]() ,则
,则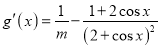 ,
,
设![]() ,则
,则![]() ,
,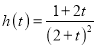 ,
,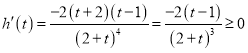 ,
,
所以![]() 在
在![]() 上递增,所以
上递增,所以![]() 的值域为
的值域为![]() ,
,
①当![]() ,即
,即![]() 时,
时,![]() ,
,![]() 为
为![]() 上的增函数,
上的增函数,
所以![]() ,符合条件;
,符合条件;
②当![]() ,即
,即![]() 时,
时,![]() ,
,![]() 为
为![]() 上的减函数,
上的减函数,
所以当![]() 时,
时,![]() ,不符合条件,舍去;
,不符合条件,舍去;
③当![]() ,即
,即![]() 时,存在
时,存在![]() ,使
,使![]() ,且
,且![]() 时,
时,![]() ,此时
,此时![]() ,不符合条件,舍去
,不符合条件,舍去
综上,所求的m的取值范围为![]() .
.

练习册系列答案
相关题目
【题目】已知某种新型病毒的传染能力很强,给人们生产和生活带来很大的影响,所以创新研发疫苗成了当务之急.为此,某药企加大了研发投入,市场上这种新型冠状病毒的疫苗![]() 的研发费用
的研发费用![]() (百万元)和销量
(百万元)和销量![]() (万盒)的统计数据如下:
(万盒)的统计数据如下:
研发费用 | 2 | 3 | 6 | 10 | 13 | 14 |
销量 | 1 | 1 | 2 | 2.5 | 4 | 4.5 |
(1)根据上表中的数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (用分数表示);
(用分数表示);
(2)根据所求的回归方程,估计当研发费用为1600万元时,销售量为多少?
参考公式: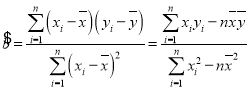 ,
,![]() .
.