题目内容
14．已知函数f（x）=$\left\{\begin{array}{l}{-\frac{1}{2}x+\frac{1}{2}}&{（x≤-1）}\\{{x}^{2}}&{（-1＜x＜1）}\\{\frac{1}{2}x+\frac{1}{2}}&{（x≥1）}\end{array}\right.$（1）求f（-2），f（0），f（2）的值
（2）作出函数f（x）的简图．
分析 （1）根据已知中函数f（x）=$\left\{\begin{array}{l}{-\frac{1}{2}x+\frac{1}{2}}&{（x≤-1）}\\{{x}^{2}}&{（-1＜x＜1）}\\{\frac{1}{2}x+\frac{1}{2}}&{（x≥1）}\end{array}\right.$，将x=-2，0，2，代入可得对应的函数值；
（2）根据一次函数和二次函数的图象和性质，画出三段上函数的图象，可得答案．
解答 解：（1）∵函数f（x）=$\left\{\begin{array}{l}{-\frac{1}{2}x+\frac{1}{2}}&{（x≤-1）}\\{{x}^{2}}&{（-1＜x＜1）}\\{\frac{1}{2}x+\frac{1}{2}}&{（x≥1）}\end{array}\right.$，
∴f（-2）=$\frac{3}{2}$，f（0）=0，f（2）=$\frac{3}{2}$，
（2）函数f（x）的简图如下图所示：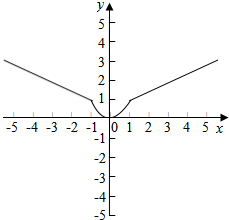
点评 本题考查的知识点是分段函数的应用，一次函数和二次函数的图象和性质，难度不大，属于基础题．
练习册系列答案
相关题目
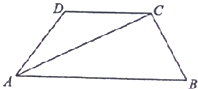如图，在梯形ABCD中，AB∥CD，且AB=2CD，设$\overrightarrow{AD}$=$\overrightarrow{a}$，$\overrightarrow{BC}$=$\overrightarrow{b}$．
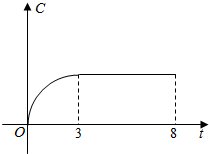某工厂近8年来产品总量C与时间t（年）的关系如图所示，则下列说法中正确的序号是②③．
4．已知锐角△ABC中，A=2B，AC=2，则BC的范围为（ ）
| A． | （2$\sqrt{2}$，2$\sqrt{3}$） | B． | （$\sqrt{2}$，$\sqrt{3}$） | C． | （$\frac{\sqrt{2}}{2}$，$\frac{\sqrt{3}}{2}$） | D． | [2$\sqrt{2}$，2$\sqrt{3}$] |