题目内容
已知直线l经过点P（－2，5），且斜率为
（1）求直线l的方程；
（2）求与直线l切于点（2，2），圆心在直线
上的圆的方程.
（1）求直线l的方程；
（2）求与直线l切于点（2，2），圆心在直线
上的圆的方程.（1）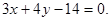
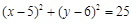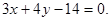；（2）
.
；（2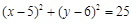）.试题分析：（1）根据点斜式方程
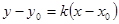,即可求出直线方程；（2）先求圆心，利用过点
与直线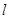
垂直的直线必过圆心，圆心在直线
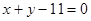上，求出圆心，然后圆心与点的距离等于半径，即可得到圆的方程..解：（1）由直线方程的点斜式，得
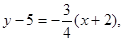整理，得所求直线方程为 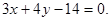4分（2）过点（2，2）与l垂直的直线方程为
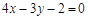， 6分由
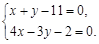得圆心为（5，6）， 8分∴半径
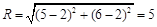， 10分故所求圆的方程为
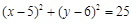． 12分
练习册系列答案
相关题目
作一直线
，使它被两直线
和
所截的线段
以
为中点，求此直线
的方程．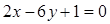
并且与曲线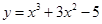
相切的直线方程.
表示的直线是( )
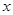与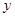
都是整数，就称点
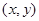为整点，命题：
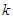与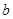
都是无理数，则直线
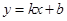不经过任何整点；
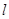经过两个不同的整点，则
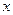轴上，C1的中心和C2的顶点均为原点，从每条曲线上各取两点，将其坐标记录于下表中：
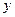
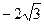
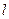与椭圆C1交于不同两点M、N，且
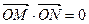。请问是否存在直线
，圆M的方程为
，过圆M上任意一点P做圆O的切线PA，若直线PA与圆M的另一个交点为Q，则当弦PQ的长度最大时，直线PA的斜率为 （ ）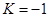
或
或
，且被两直线L1：
和 L2：
截得的线段AB中点恰好是点P，求直线L的方程．