题目内容
.(本小题满分14分)已知函数 (
( ,
, 是不同时为零的常数),其导函数为
是不同时为零的常数),其导函数为 .
.
(1)当 时,若不等式
时,若不等式 对任意
对任意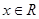 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(2)求证:函数 在
在 内至少存在一个零点;
内至少存在一个零点;
(3)若函数 为奇函数,且在
为奇函数,且在 处的切线垂直于直线
处的切线垂直于直线 ,关于
,关于 的方程
的方程 在
在 上有且只有一个实数根,求实数
上有且只有一个实数根,求实数 的取值范围.
的取值范围.
【答案】
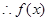 在
在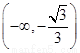 ,
,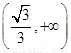 上是单调递增函数,在
上是单调递增函数,在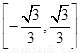 上是单调递减函数,由
上是单调递减函数,由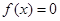 解得
解得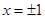 ,
, ,
,




 即
即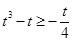 ,解得
,解得 ;
;



②当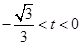 时,
时,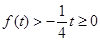 ,
,
③当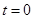 时,显示不成立;
时,显示不成立;







④当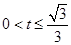 时,
时,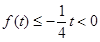 ,
,





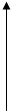
即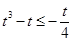 ,解得
,解得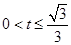 ;
;

 ⑤当
⑤当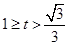 时,
时, ,
,
解得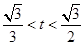 ;
;

 ⑥当
⑥当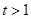 时,
时,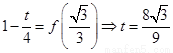 .
.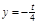
解:(1)当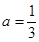 时,
时,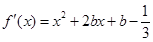 ,………1分
,………1分
依题意 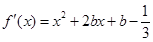
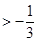 即
即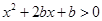 恒成立
恒成立
 ,解得
,解得 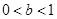
所以b的取值范围是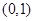 …………………………………4分
…………………………………4分
(2)证明:因为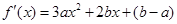 ,
,
解法一:当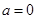 时,
时,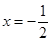 符合题意. ……………………………5分
符合题意. ……………………………5分
当 时,
时,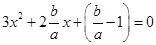 ,令
,令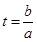 ,则
,则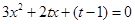 ,
,
令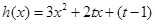 ,
,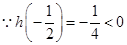 , 当
, 当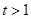 时,
时,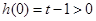 ,
,
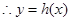 在
在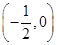 内有零点;……………………………7分
内有零点;……………………………7分
当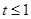 时,
时, ,
,
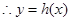 在
在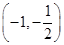 内有零点.
内有零点.
 当
当 时,
时,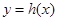 在
在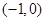 内至少有一个零点.
内至少有一个零点.
综上可知,函数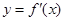 在
在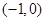 内至少有一个零点. ……………………………9分
内至少有一个零点. ……………………………9分
解法二: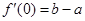 ,
,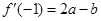 ,
,
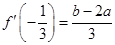 .
.
因为a,b不同时为零,所以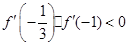 ,故结论成立.
,故结论成立.
(3)因为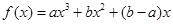 为奇函数,所以
为奇函数,所以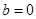 ,所以
,所以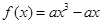 ,
, .
.
又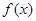 在
在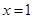 处的切线垂直于直线
处的切线垂直于直线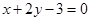 ,所以
,所以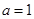 ,即
,即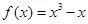 .
.
……………………………………………………………………………………10分
|
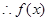 在
在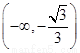 ,
,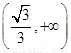 上是单调递增函数,在
上是单调递增函数,在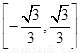 上是单调递减函数,由
上是单调递减函数,由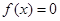 解得
解得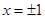 ,
, ,
,
法一:如图所示,作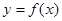 与
与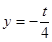 的图像,若只有一个交点,则
的图像,若只有一个交点,则
 ①当
①当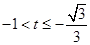 时,
时,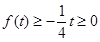 ,
,
|
|




|
|
 即
即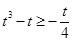 ,解得
,解得 ;
;



|
|


|
|

|
|
|
|
|
|
|
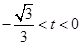 时,
时,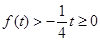 ,
,
 解得
解得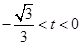 ;
;
|
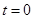 时,显示不成立;
时,显示不成立;
|



|


|

|
|

|
|
|
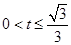 时,
时,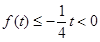 ,
,
|
|
|
|



|


|
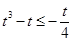 ,解得
,解得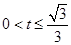 ;
;
|
|

 ⑤当
⑤当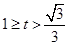 时,
时, ,
,


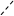




|
|
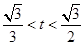 ;
;
|
|

|
 ⑥当
⑥当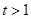 时,
时,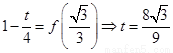 .
.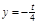
………………………………………………………………13分
综上t的取值范围是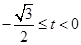 或
或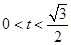 或
或 .………………14分
.………………14分
法二:由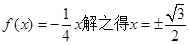 ,
, .
.
作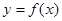 与
与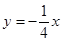 的图知交点横坐标为
的图知交点横坐标为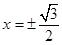 ,
,
当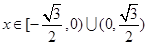
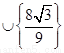 时,过
时,过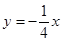 图象上任意一点向左作平行于
图象上任意一点向左作平行于 轴的直线与
轴的直线与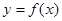 都只有唯一交点,当
都只有唯一交点,当 取其它任何值时都有两个或没有交点。
取其它任何值时都有两个或没有交点。
所以当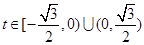
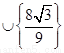 时,方程
时,方程 在
在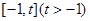 上有且只有一个实数根.
上有且只有一个实数根.
【解析】略

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
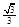
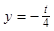
 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)