题目内容
16．如图，在边长为3的正方形ABCD中，AC与BD交于F，AE=$\frac{1}{3}$AD，则$\overrightarrow{EF}•\overrightarrow{BD}$=-3．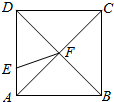
分析 由题意，可建立以AB所在直线为X轴，以AD所在直线为Y轴建立平面直角坐标系，利用向量的坐标，再求$\overrightarrow{EF}•\overrightarrow{BD}$的值．
解答 解：由题设，可以AB所在直线为X轴，以AD所在直线为Y轴建立平面直角坐标系，
故有A（0，0），B（3，0），C（3，3），D（0，3），E（0，1），F（1.5.1.5）．
则$\overrightarrow{EF}•\overrightarrow{BD}$=（1.5，0.5）•（-3，3）=-4.5+1.5=-3，
故答案为：-3．
点评 本题考查了数量积的坐标运算，考查学生的计算能力，综合性较强，
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
相关题目
6．设a，b是非零实数，且满足$\frac{asin\frac{π}{5}+bcos\frac{π}{5}}{acos\frac{π}{5}-bsin\frac{π}{5}}$=tan$\frac{8π}{15}$，若类比两角和的正切公式，则$\frac{b}{a}$=（ ）
| A． | 4 | B． | $\sqrt{15}$ | C． | 2 | D． | $\sqrt{3}$ |
4．已知角α的终边经过点P（-1，2），则tan（α+$\frac{π}{4}$）的值是（ ）
| A． | 3 | B． | -3 | C． | $\frac{1}{3}$ | D． | -$\frac{1}{3}$ |
中心在原点、焦点在x轴上的椭圆与双曲线有公共焦点，左右焦点分别为F1、F2，且它们在第一象限的交点为P，△PF1F2是以PF2为底边的等腰三角形．若|PF2|=10，双曲线离心率的取值范围为（1，2），则椭圆离心率的取值范围是（$\frac{2}{3}$，1）．