题目内容
数列{an}的前n项和为Sn,已知 ,数列{bn}满足
,数列{bn}满足 且b2=4,b5=32.
且b2=4,b5=32.(1)分别求出数列{an}和数列{bn}的通项公式;
(2)若数列{cn}满足
 ,求数列{cn}的前n项和Tn;
,求数列{cn}的前n项和Tn;(3)设
 ,当n为奇数时,试判断方程Tn-P=2013是否有解,若有请求出方程的解,若没有,请说明理由.
,当n为奇数时,试判断方程Tn-P=2013是否有解,若有请求出方程的解,若没有,请说明理由.
【答案】分析:(1)利用数列和与通项的关系,可求数列{an}的通项公式;确定{bn}为等比数列,可得数列{bn}的通项公式;
(2)分n为偶数与奇数,利用分组求和法,分别求和,可得结论;
(3)确定n≥5时,f(n)=Tn-P单调递增,计算相应函数值,可得结论.
解答:解:(1)当n=1时,a1=S1=2,
当n≥2时, ,所以an=n+1(n≥2)
,所以an=n+1(n≥2)
又n=1时,n+1=2=a1,所以 …(2分)
…(2分)
因为 ,所以{bn}为等比数列 …(3分)
,所以{bn}为等比数列 …(3分)
又b2=4,b5=32,所以公比为2,首项为2,所以 …(4分)
…(4分)
(2)当n为偶数时,Tn=(a1+a3+…+an-1)+(b2+b4+…+bn)
= …(6分)
…(6分)
当n为奇数时,n+1为偶数,
所以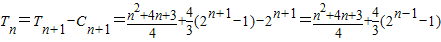 …(8分)
…(8分)
即 …(9分)
…(9分)
(3)设 …(10分)
…(10分)
∴ …(11分)
…(11分)
∴当x≥5时,f(n+2)-f(n)=2n+1-46>0,此时f(n)单调递增.
又 ,
,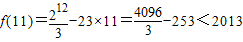 ,
,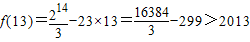 …(13分)
…(13分)
所以原方程无解.…(14分)
点评:本题考查数列的通项与求和,考查数列的单调性,考查学生分析解决问题的能力,掌握数列的求和方法是关键.
(2)分n为偶数与奇数,利用分组求和法,分别求和,可得结论;
(3)确定n≥5时,f(n)=Tn-P单调递增,计算相应函数值,可得结论.
解答:解:(1)当n=1时,a1=S1=2,
当n≥2时,
 ,所以an=n+1(n≥2)
,所以an=n+1(n≥2)又n=1时,n+1=2=a1,所以
 …(2分)
…(2分)因为
 ,所以{bn}为等比数列 …(3分)
,所以{bn}为等比数列 …(3分)又b2=4,b5=32,所以公比为2,首项为2,所以
 …(4分)
…(4分)(2)当n为偶数时,Tn=(a1+a3+…+an-1)+(b2+b4+…+bn)
=
 …(6分)
…(6分)当n为奇数时,n+1为偶数,

所以
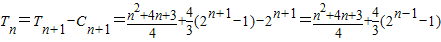 …(8分)
…(8分)即
 …(9分)
…(9分)(3)设
 …(10分)
…(10分)∴
 …(11分)
…(11分)∴当x≥5时,f(n+2)-f(n)=2n+1-46>0,此时f(n)单调递增.
又
 ,
,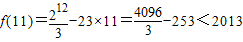 ,
,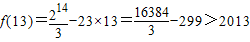 …(13分)
…(13分)所以原方程无解.…(14分)
点评:本题考查数列的通项与求和,考查数列的单调性,考查学生分析解决问题的能力,掌握数列的求和方法是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目