题目内容
【题目】如图,四棱锥P-ABCD中,底面ABCD是边长为3的菱形,∠ABC=60°.PA⊥面ABCD,且PA=3.F在棱PA上,且AF=1,E在棱PD上.
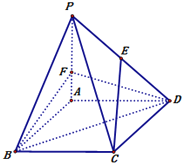
(Ⅰ)若CE∥面BDF,求PE:ED的值;
(Ⅱ)求二面角B-DF-A的大小.
【答案】(Ⅰ)见解析;(Ⅱ)arctan![]()
【解析】
(Ⅰ)根据线面平行的性质定理进行推理得到E为PD中点即可求PE:ED的值;
(Ⅱ)根据二面角的定义作出二面角的平面角,即可求二面角B﹣DF﹣A的大小.
(Ⅰ)过E作EG∥FD交AP于G,连接CG,连接AC交BD于O,连接FO.
∵EG∥FD,EG面BDF,FD面BDF,∴EG∥面BDF,又EG∩CE=E,CE∥面BDF,EG,CE面CGE,
∴面CGE∥面BDF,又CG面CGE,∴CG∥面BDF,
又面BDF∩面PAC=FO,CG面PAC,∴FO∥CG.
又O为AC中点,∴F为AG中点,且AF=1,∴AF=FG=1,∵PA=3,∴FG=GP=1,
∴E为PD中点,PE:ED=1:1.
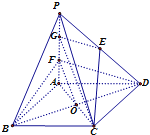
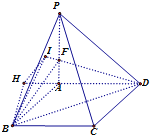
(Ⅱ)过点B作BH⊥直线DA交DA延长线于H,过点H作HI⊥直线DF交DF于I,
∵PA⊥面ABCD,∴面PAD⊥面ABCD,∴BH⊥面PAD,由三垂线定理可得DI⊥IB,
∴∠BIH是二面角B-DF-A的平面角.由题易得AH=![]() ,BH=
,BH=![]() ,HD=
,HD=![]() ,
,
且![]() =
=![]() ,∴HI=
,∴HI=![]() ,∴tan∠BIH=
,∴tan∠BIH=![]() ×
×![]() =
=![]() ,
,
∴二面角B-DF-A的大小为arctan![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目