题目内容
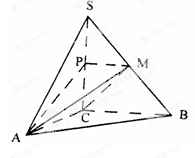
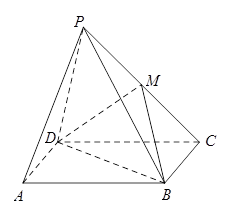
如图,四棱锥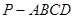 中,底面
中,底面 为梯形,
为梯形,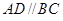 ,
,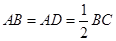 ,
, ,平面
,平面 平面
平面 ,
, .
.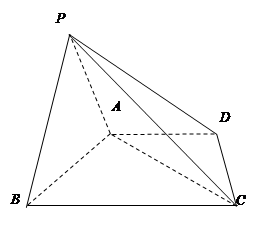
(1)求证: 平面
平面 ;
;
(2)求证: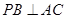 ;
;
(3)是否存在点 ,到四棱锥
,到四棱锥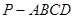 各顶点的距离都相等?并说明理由.
各顶点的距离都相等?并说明理由.
(1)参考解析;(2)参考解析;(3)存在
解析试题分析:(1)线面平面平行的证明,关键是在平面内找到一条直线与要证明的直线平行,根据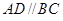 ,再根据直线BC,直线AD的位置关系,即可得线面平行.线面平行还有一种就是转化为面面平行.线面平行的证明就是这两种判断的相互转化.
,再根据直线BC,直线AD的位置关系,即可得线面平行.线面平行还有一种就是转化为面面平行.线面平行的证明就是这两种判断的相互转化.
(2)要证线线垂直转化为线面垂直,由题意可知,通过证明直线AC垂直于平面PAB,由面面垂直可知,只需证明直线AC垂直于AB,在三角形ABC中,由所给条件即可得到AC垂直于AB.
(3)由(2)可知直线PB垂直于平面PAC.所以可得直线PB垂直于直线PC.通过三角形的BCD全等于三角形CBA,所以可得直线BD垂直于DC.所以BC是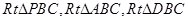 的斜边,即BC的中点就是所要找的Q点.
的斜边,即BC的中点就是所要找的Q点.
试题解析:(1)证明:底面 为梯形,
为梯形,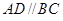 ,
,
又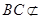 平面
平面 ,
,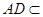 平面
平面 ,
,
所以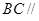 平面
平面 .
.
(2)证明:设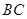 的中点为
的中点为 ,连结
,连结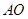 ,在梯形
,在梯形 中,
中,
因为 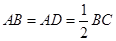 ,
, ,
,
所以 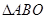 为等边三角形,
为等边三角形,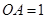 ,
,
又 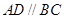 ,
,
所以 四边形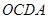 为菱形.
为菱形.
因为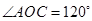 ,
,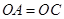 ,
,
所以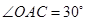 ,
,
所以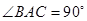 ,
,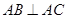 ,
,
又平面 平面
平面 ,
,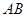 是交线,
是交线,
所以 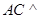 平面
平面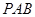 ,
,
所以 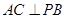 ,即
,即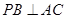 .
.
(3)解:因为 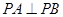 ,
,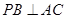 ,所以
,所以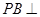 平面
平面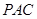 .
.
所以,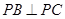 ,
,
所以 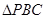 为直角三角形,
为直角三角形,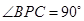 .
.
连结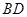 ,由(2)知
,由(2)知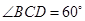 ,
,
所以 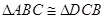 ,
,
所以 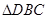 为直角三角形,
为直角三角形,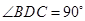 .
.
所以点 是三个直角三角形:
是三个直角三角形: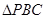 、
、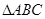 和
和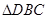 的共同的斜边
的共同的斜边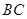 的中点,
的中点,
所以 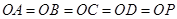 ,
,
所以存在点 (即点
(即点 )到四棱锥
)到四棱锥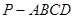 各顶点的距离都相等.
各顶点的距离都相等.
考点:1.线面平行的判定.2.线线垂直的判定.3.直角三形的性质.4.归纳推理论证的能力.

练习册系列答案
相关题目
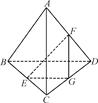
 中,
中, ,点
,点 是
是 的中点。
的中点。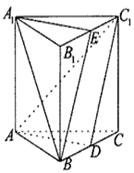
 ∥平面
∥平面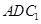
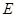 是
是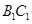 的中点,求证:平面
的中点,求证:平面 平面
平面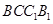 .
.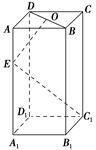
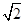 ,OE⊥EC1,求AA1的长.
,OE⊥EC1,求AA1的长.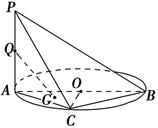
 为直角三角形,
为直角三角形,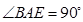 ,且
,且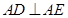 .
.
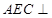 平面
平面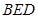 ;
;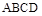 与
与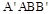 都是边长为
都是边长为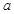 的正方形,点E是
的正方形,点E是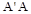 的中点,
的中点,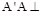 平面
平面
 平面
平面 ;
; 平面
平面