题目内容
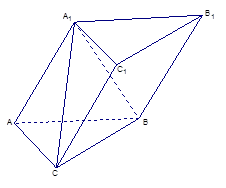
如图,在直三棱柱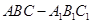 中,
中,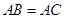 ,点
,点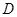 是
是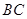 的中点。
的中点。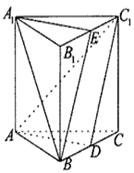
(1)求证: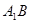 ∥平面
∥平面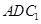
(2)如果点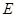 是
是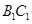 的中点,求证:平面
的中点,求证:平面 平面
平面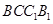 .
.
(1)详见解析;(2)详见解析
解析试题分析:(1)证明A1B∥平面ADC1,利用线面平行的判定,只需证明A1B∥OD即可
(2)证明平面A1BE⊥平面BCC1B1,利用面面垂直的判定,证明A1E⊥平面BCC1B1即可.
试题解析:连接A1C交AC1与点O,连结OD。
在△A1BC中A1B∥OD。又OD在面ADC1内,A1B不在面ADC1内,所以A1B∥平面ADC1
直三棱柱ABC-A1B1C1中,C1C⊥平面ABC,
∴C1C⊥AD,又在△ABC中AD⊥BC,
∴AD⊥平面BCC1B1,连接DE,∵E点是B1C1的中点,∴在直三棱柱ABC-A1B1C1中,四边形B1BDE为平行四边形,∴B1B∥ED,B1B=ED,又B1B∥A1A,B1B=A1A,∴ED∥A1A,∴四边形A1ADE为平行四边形,
∴A1E∥AD,于是A1E垂直平面BCC1B1,又A1E在面A1BE内,所以平面A1BE⊥平面BCC1B1
考点:空间线面位置关系的证明.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
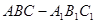 中,四边形
中,四边形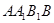 是菱形,四边形
是菱形,四边形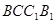 是矩形,
是矩形,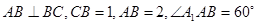 .
.
 ;
;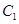 到平面
到平面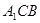 的距离;
的距离;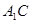 与平面
与平面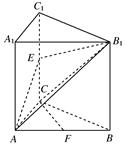

 的值.
的值. 中
中 ,平面
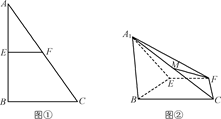
,平面 外一条线段AB满足AB∥DE,AB
外一条线段AB满足AB∥DE,AB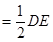 ,AB⊥AC,F是CD的中点.
,AB⊥AC,F是CD的中点.
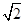 .
.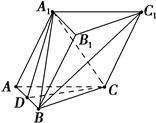
 中,底面
中,底面 为梯形,
为梯形,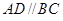 ,
,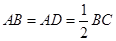 ,
, ,平面
,平面 平面
平面 .
.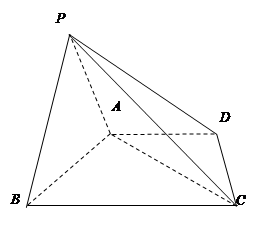
 平面
平面 ;
;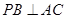 ;
; ,到四棱锥
,到四棱锥 中, 底面四边形
中, 底面四边形 是直角梯形,
是直角梯形, 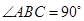 ,
,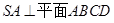 ,
, .
.
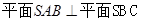 ;
; 与底面
与底面