已知A是△BCD平面外的一点.E.F分别是BC.AD的中点． (1)求证:直线EF与BD是异面直线,(2)若AC⊥BD.AC＝BD.求EF与BD所成的角．题目和参考答案——青夏教育精英家教网——

题目内容

已知A是△BCD平面外的一点，E，F分别是BC，AD的中点．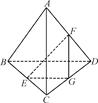

(1)求证：直线EF与BD是异面直线；
(2)若AC⊥BD，AC＝BD，求EF与BD所成的角．

（1）见解析（2）45°

解析

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

如图，三棱柱的底面是边长为2的正三角形，且侧棱垂直于底面，侧棱长是，D是AC的中点。

（1）求证：平面；
（2）求二面角的大小；
（3）求直线与平面所成的角的正弦值.

如图①，E、F分别是直角三角形ABC边AB和AC的中点，∠B＝90°，沿EF将三角形ABC折成如图②所示的锐二面角A₁EFB，若M为线段A₁C中点．求证：

(1)直线FM∥平面A₁EB；
(2)平面A₁FC⊥平面A₁BC.

如图所示，在正方体ABCDA₁B₁C₁D₁中，E、F、G、H分别是BC、CC₁、C₁D₁、A₁A的中点．求证：

(1)BF∥HD₁；
(2)EG∥平面BB₁D₁D.

如图，在四棱锥PABCD中，底面ABCD是正方形，侧面PAD⊥底面ABCD，且PA＝PD＝ AD.若E、F分别为PC、BD的中点，求证：

(1)EF∥平面PAD；
(2)EF⊥平面PDC.

正三棱柱ABCA₁B₁C₁中，已知AB＝A₁A，D为C₁C的中点，O为A₁B与AB₁的交点．

(1)求证：AB₁⊥平面A₁BD；
(2)若点E为AO的中点，求证：EC∥平面A₁BD.

如图，棱柱中，四边形是菱形，四边形是矩形，.

（1）求证：平面；
（2）求点到平面的距离；
（3）求直线与平面所成角的正切值.

如图，三棱柱ABC－A₁B₁C₁的侧棱AA₁⊥底面ABC，∠ACB＝90°，E是棱CC₁的中点，F是AB的中点，AC＝BC＝1，AA₁＝2.

(1)求证：CF∥平面AB₁E；
(2)求三棱锥C－AB₁E在底面AB₁E上的高．

如图，四棱锥中，底面为梯形，，，，平面平面，．

（1）求证：平面；
（2）求证：；
（3）是否存在点，到四棱锥各顶点的距离都相等？并说明理由.