题目内容
如图,在四棱锥P-ABCD中,四边形ABCD是矩形,平面PCD⊥平面ABCD,M为PC中点.求证: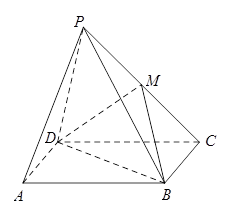
(1)PA∥平面MDB;
(2)PD⊥BC.
(1)详见解析;(2)详见解析.
解析试题分析:(1)线面平行的判定关键在证相应线线平行,线线平行的证明或寻求需要结合平面几何的知识,如中位线平行于底面,因为本题中M为PC中点,所以应取BD的中点作为解题突破口;(2)线线垂直的证明一般需要经过多次线线垂直与线面垂直的转化,而对于面面垂直,基本是单向转化,即作为条件,就将其转化为线面垂直;作为结论,只需寻求线面垂直. 如本题中面PCD与面ABCD垂直,就转化为BC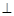 平面PCD,到此所求问题转化为:已知线面垂直,要求证线线垂直.在线线垂直与线面垂直的转化过程中,要注意充分应用平面几何中的垂直条件,如矩形邻边相互垂直.
平面PCD,到此所求问题转化为:已知线面垂直,要求证线线垂直.在线线垂直与线面垂直的转化过程中,要注意充分应用平面几何中的垂直条件,如矩形邻边相互垂直.
试题解析:证明:(1)连结AC交BD于点O,连结OM. 2分
因为M为PC中点,O为AC中点,
所以MO//PA. 4分
因为MO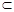 平面MDB,PA
平面MDB,PA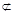 平面MDB,
平面MDB,
所以PA//平面MDB. 7分
(2)因为平面PCD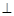 平面ABCD,
平面ABCD,
平面PCD 平面ABCD=CD,
平面ABCD=CD,
BC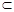 平面ABCD,BC
平面ABCD,BC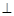 CD,
CD,
所以BC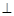 平面PCD. 12分
平面PCD. 12分
因为PD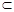 平面PCD,
平面PCD,
所以BC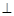 PD 14分
PD 14分
考点:直线与平面平行判定定理,面面垂直性质定理.

练习册系列答案
相关题目
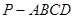 中,底面
中,底面 为梯形,
为梯形,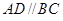 ,
,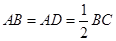 ,
, ,平面
,平面 平面
平面 .
.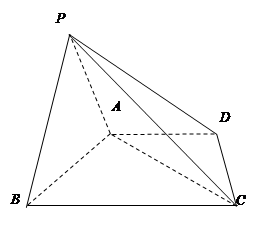
 平面
平面 ;
;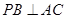 ;
; ,到四棱锥
,到四棱锥 中, 底面四边形
中, 底面四边形 是直角梯形,
是直角梯形, 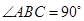 ,
,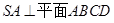 ,
, .
.
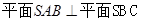 ;
; 与底面
与底面 .
.
 的边长为3,点
的边长为3,点 、
、 分别是边
分别是边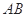 、
、 上的点,且满足
上的点,且满足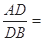
 (如图1).将△
(如图1).将△ 沿
沿 折起到△
折起到△ 的位置,使二面角
的位置,使二面角 为直二面角,连结
为直二面角,连结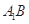 、
、 (如图2).
(如图2).
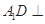 平面
平面 ;
;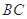 上是否存在点
上是否存在点 ,使直线
,使直线 与平面
与平面 所成的角为
所成的角为 ?若存在,求出
?若存在,求出 的长,若不存在,请说明理由.
的长,若不存在,请说明理由. 所在平面与正
所在平面与正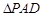 所在平面互相垂直,
所在平面互相垂直,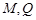 分别为
分别为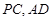 的中点.
的中点.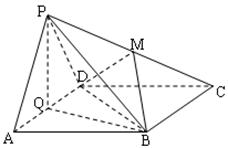
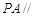 平面
平面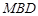 ;
;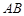 上是否存在一点
上是否存在一点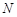 ,使得平面
,使得平面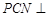 平面
平面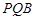 ?若存在,试指出点
?若存在,试指出点 中,
中,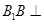 平面
平面 ,
, ,
,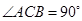 ,
, 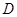 ,
, 分别是
分别是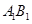 ,
, 的中点.
的中点.
 ∥平面
∥平面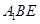 ;
; 平面
平面 ;
;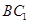 与平面
与平面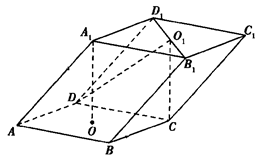
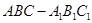 中,
中,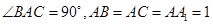 ,
,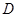 是棱
是棱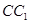 上的一点,
上的一点,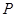 是
是 的延长线与
的延长线与 的延长线的交点,且
的延长线的交点,且 ∥平面
∥平面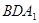 。
。
 ;
; 的平面角的余弦值;
的平面角的余弦值; 到平面
到平面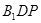 的距离.
的距离.