题目内容
9.已知f(x)的导数f′(x)=3x2-3ax,f(0)=b,a、b∈R,1<a<2(1)若函数f(x)在[-1,1]上的最小值为-2,最大值为1,求a、b.
(2)设函数F(x)=(f′(x)+6x+1)•e2x,试确定F(x)的极值点个数.
分析 (1)由题意得f(x)=x3-$\frac{3}{2}$ax2+b,从而可得fmax(x)=f(0)=b=1,f(-1)=-1-$\frac{3}{2}$a+1=-2,从而解得.
(2)求导F′(x)=e2x(6x2-(6a-18)x-3a+8),从而判断判别式即可.
解答 解:(1)∵f′(x)=3x2-3ax,f(0)=b,
∴f(x)=x3-$\frac{3}{2}$ax2+b,
∵f′(x)=3x2-3ax=3x(x-a),又∵1<a<2,
∴f(x)在[-1,0]上是增函数,在(0,1]上是减函数,
∴fmax(x)=f(0)=b=1,
又∵f(-1)=-1-$\frac{3}{2}$a+b,f(1)=1-$\frac{3}{2}$a+b,
∴f(-1)=-1-$\frac{3}{2}$a+1=-2,
∴a=$\frac{4}{3}$;
(2)F(x)=(f′(x)+6x+1)•e2x
=(3x2-3ax+6x+1)•e2x,
F′(x)=[2(3x2-3ax+6x+1)+(6x-3a+6)]•e2x
=e2x(6x2-(6a-18)x-3a+8),
∵△=(6a-18)2-4×6×(-3a+8)
=36(a2-6a+9)-24(-3a+8)
=6(6a2-36a+54+12a-32)
=12(3a2-12a+11)=12[3(a-2)2-1],
当2-$\frac{\sqrt{3}}{3}$≤a<2时,△≤0,F(x)没有极值点;
当1<a<2-$\frac{\sqrt{3}}{3}$,△>0,F′(x)=0有两个不同的根,
故F(x)有两个极值点.
点评 本题考查了导数的综合应用及函数的极值的个数的确定.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.某校企合作工厂机床的生产数量x(百台)与生产成本y(万元)之间有着一定的函数关系,在经济学中称为成本函数,记为C(x).已知这个函数是一元二次函数y=ax2+bx+c(a≠0),且机床的收益函数R(x)=18.5x.经实际测算得到下列数据:
(1)求利润函数L(x):[提示:利润函数L(x)=R(x)-C(x)]
(2)若企业盈利,试求生产数量x的范围.
| 产品数量x | 0 | 3 | 4 | 6 | 7.2 | 10 |
| 生产成本y | 50 | 72.5 | 82 | 104 | 119.2 | 160 |
(2)若企业盈利,试求生产数量x的范围.
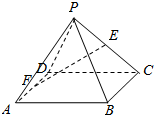 如图,四棱锥P-ABCD中,ABCD为矩形,面PDC⊥面ABCD,∠DPC=90°,E,F 分别为PC,AD的中点.
如图,四棱锥P-ABCD中,ABCD为矩形,面PDC⊥面ABCD,∠DPC=90°,E,F 分别为PC,AD的中点.