��Ŀ����
����Ŀ��2016��ij��Ϊ�˴ٽ����������ķ��ദ����������������Ϊ�����������ɻ�����������������࣬���ֱ���������Ӧ�������䣮Ϊ�������������������Ͷ��������������ȡ�˸����������������ܼ�60�ֳ���������������������ڡ������������䡢���ɻ������͡��������������Ͷ�����ֱ�Ϊx��y��z������x��0��x+y+z=60��������x��y��z�ı�������ֵΪ �� ��ע������ ![]() ������
������ ![]() Ϊx1 �� x2 �� ����xn��ƽ������
Ϊx1 �� x2 �� ����xn��ƽ������
���𰸡�20 ![]()
���������⣺�������֪����x+y+z=60�� ��x��y��z��ƽ����Ϊ20
��s2= ![]() [��x��20��2+��y��20��2+��z��20��2]=
[��x��20��2+��y��20��2+��z��20��2]= ![]() ��x2+y2+z2��1200����
��x2+y2+z2��1200����
�ߣ�x+y+z��2=x2+y2+z2+2xy+2yz+2xz��x2+y2+z2 ��
����е�x=60��y=0��z=0ʱ��
�������ֵs2=800��
��ʱ����x��y��z�ı�������ֵΪ20 ![]() ��
��
���Դ��ǣ�20 ![]()
�����㾫�����������⣬������Ҫ�˽⺯������ֵ���伸������(���ö��κ��������ʣ��䷽�������������С��ֵ������ͼ�����������С��ֵ�����ú��������Ե��жϺ��������С��ֵ)��

����Ŀ��ij�̳�ÿ����ÿ��100Ԫ�ļ۸���A��Ʒ���ɼ�������ÿ��200Ԫ�ļ۸���ۣ�����������A��Ʒǰ8Сʱû�����꣬���̳���û������A��Ʒ��ÿ��60Ԫ�ĵͼ۵��촦����ϣ��ٶ�A��Ʒ�����ܹ������꣩�����̳�ͳ����100��A��Ʒ��ÿ���ǰ8Сʱ�����������Ƴ������
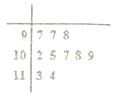
ǰ8Сʱ��������t����λ������ | 5 | 6 | 7 |
Ƶ �� | 40 | 35 | 25 |
��1����ij����̳�������7��A��Ʒ����ǰ8��Сʱ�۳�5���� ����Щ��Ʒ��7����ͬ�Ĺ˿����ִ���7���˿������ѡ3�˽��лطã���X��ʾ��3������ÿ��200Ԫ�ļ۸������������X�ķֲ��У�
��2����Ƶ����Ϊ���ʣ�Ҫʹ�̳�ÿ�칺��A��Ʒʱ����õ�ƽ�����������ÿ��Ӧ��������A��Ʒ����˵�����ɣ�