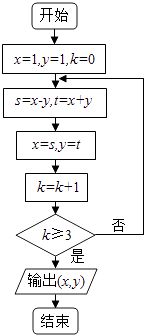
题目内容
【题目】甲、乙两人的各科成绩如茎叶图所示，则下列说法正确的是（ ） 
A.甲的中位数是89，乙的中位数是98
B.甲的各科成绩比乙各科成绩稳定
C.甲的众数是89，乙的众数是98
D.甲、乙二人的各科成绩的平均分不相同
【答案】B
【解析】解：由茎图知甲的中位数是83，乙的中位数是85，故A错误； 由由茎图知甲的数据相对集中，乙的数据相对分散，
故甲的各科成绩比乙各科成绩稳定，故B正确；
甲的众数是83，乙的众数是98，故C错误；
甲的平均数 
= 
（68+74+77+83+83+84+89+92+93）= 
，
乙的平均数 
= （64+66+74+76+85+87+98+98+95）= ，
∴甲、乙二人的各科成绩的平均分相同，故D错误．
故选：B．
【考点精析】关于本题考查的茎叶图，需要了解茎叶图又称“枝叶图”，它的思路是将数组中的数按位数进行比较，将数的大小基本不变或变化不大的位作为一个主干（茎），将变化大的位的数作为分枝（叶），列在主干的后面，这样就可以清楚地看到每个主干后面的几个数，每个数具体是多少才能得出正确答案．
【题目】已知某企业近3年的前7个月的月利润（单位：百万元）如下面的折线图所示：
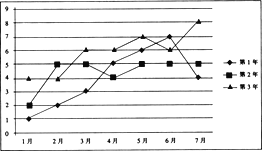
（1）试问这3年的前7个月中哪个月的月平均利润最高？
（2）通过计算判断这3年的前7个月的总利润的发展趋势；
（3）试以第3年的前4个月的数据（如下表），用线性回归的拟合模式估测第3年8月份的利润．
月份x | 1 | 2 | 3 | 4 |
利润y（单位：百万元） | 4 | 4 | 6 | 6 |
相关公式：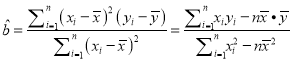 
， 
．
【题目】为了解某班学生喜爱打篮球是否与性别有关，对本班
人进行了问卷调查得到了如下的列联表：已知在全部
人中随机抽取
人,抽到喜爱打篮球的学生的概率为
．
（1）请将上面的列联表补充完整(不用写计算过程)；并求出：有多大把握认为喜爱打篮球与性别有关，说明你的理由；
（2）若从该班不喜爱打篮球的男生中随机抽取3人调查，求其中某男生甲被选到的概率。下面的临界值表供参考：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5. 024 | 6.635 | 7.879 | 10.828 |
(参考公式： 
，其中
)
