题目内容
已知函数y=f（x）的大致图象如图所示，则函数y=f（x）的解析式应为（ ）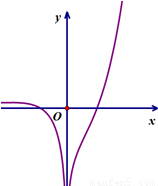
A．f（x）=exln
B．f（x）=e-xln|x|
C．f（x）=exln|x|
D．f（x）=e|x|ln|x|
【答案】分析：本题是选择题，可采用排除法，根据函数的不关于y轴对称可排除选项D，再根据函数定义域是{x|x≠0}，排除选项A，利用极限思想可排除B，即可得到所求．
解答：解：如图，因为函数定义域是{x|x≠0}，排除A选项，
当x→-∞，f（x）→0，排除B，
根据函数图象不关于y轴对称可知函数不是偶函数，故可排除选项D，
故选C．
点评：本题主要考查了识图能力，以及函数的对称性和单调性，数形结合的思想，属于基础题．
解答：解：如图，因为函数定义域是{x|x≠0}，排除A选项，
当x→-∞，f（x）→0，排除B，
根据函数图象不关于y轴对称可知函数不是偶函数，故可排除选项D，
故选C．
点评：本题主要考查了识图能力，以及函数的对称性和单调性，数形结合的思想，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
已知函数y=f（x）是定义在R上的奇函数，当x＞0 时，f（x）的图象如图所示，则不等式x[f（x）-f（-x）]≤0 的解集为
已知函数y=f（x）的图象如图，则满足