题目内容
抛物线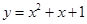 在点(0,1)处的切线方程为
在点(0,1)处的切线方程为
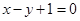 (或y=x+1)
(或y=x+1)
解析试题分析:因为抛物线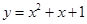 的导数值为y’=2x+1,那么可知在x=0处的导数值为1,可知该点的切线的斜率为1,点斜式方程可知为y-1=x-0,故可知y=x+1.答案为y=x+1
的导数值为y’=2x+1,那么可知在x=0处的导数值为1,可知该点的切线的斜率为1,点斜式方程可知为y-1=x-0,故可知y=x+1.答案为y=x+1
考点:本题主要考查了导数几何意义的运用。
点评:解决该试题的关键是求解导数,并利用导数的几何意义,在某点的导数值即为该点的切线的斜率。

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
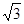 ) ,渐近线方程为
) ,渐近线方程为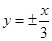 ,则此双曲线的方程为 _.
,则此双曲线的方程为 _.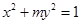 的离心率为
的离心率为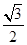 ,则它的长半轴长为_______
,则它的长半轴长为_______ 的左、右焦点分别为
的左、右焦点分别为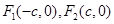 ,若椭圆上存在一点
,若椭圆上存在一点 使
使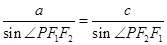 ,则该椭圆的离心率的取值范围为 .
,则该椭圆的离心率的取值范围为 .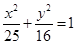 的左、右焦点,P为椭圆上任一点,点M的坐标为(6,4),则|PM|+|PF1|的最大值为 .
的左、右焦点,P为椭圆上任一点,点M的坐标为(6,4),则|PM|+|PF1|的最大值为 .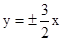 ,则其离心率是为 .
,则其离心率是为 . 的准线与x轴交于点Q,若过点Q的直线
的准线与x轴交于点Q,若过点Q的直线  与抛物线有公共点,则直线
与抛物线有公共点,则直线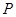 是抛物线
是抛物线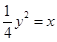 上一个动点,则点
上一个动点,则点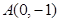 的距离与点
的距离与点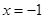 的距离和的最小值是 。
的距离和的最小值是 。