题目内容
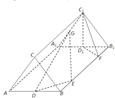 如图,在正三棱柱ABC-A1B1C1中,AA1=2AB,D,D1,G分别为AB,A1B1,A1C1的中点,E、F在BB1上,且BB1=4BE=4B1F.
如图,在正三棱柱ABC-A1B1C1中,AA1=2AB,D,D1,G分别为AB,A1B1,A1C1的中点,E、F在BB1上,且BB1=4BE=4B1F.(1)求证:DG∥平面BCC1B1;
(2)求证:平面DEG⊥平面C1D1F.
分析:(1)由题意取B1C1的中点H,连接GH、BH,只要证明四边形BDGH为平行四边形,再利用直线与平面平行的判定定理进行证明,即可解决问题;
(2)已知三棱柱ABC-A1B1C1为正三棱柱,D1分别为A1B1的中点,取BB1的中点为P,连接AP、A1P,则AP∥DE,A1P∥D1F,在等腰直角△ABP和△A1B1P中,可证AP⊥A1P,然后利用平面与平面垂直的判定定理进行证明;
(2)已知三棱柱ABC-A1B1C1为正三棱柱,D1分别为A1B1的中点,取BB1的中点为P,连接AP、A1P,则AP∥DE,A1P∥D1F,在等腰直角△ABP和△A1B1P中,可证AP⊥A1P,然后利用平面与平面垂直的判定定理进行证明;
解答: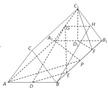 证明:(1)如图,取B1C1的中点H,连接GH、BH,
证明:(1)如图,取B1C1的中点H,连接GH、BH,
∵D,G分别为AB,A1C1的中点,
∴GH∥A1B1,GH=
A1B1,BD=
AB,
又三棱柱ABC-A1B1C1为正三棱柱,则BD∥GH,BD=GH,
故四边形BDGH为平行四边形,
∴DG∥BH,(4分)
又DG?平面BCC1B1,BH?平面BCC1B1,
∴DG∥平面BCC1B1;(6分)
(2)由三棱柱ABC-A1B1C1为正三棱柱,D1分别为A1B1的中点,
∴C1D1⊥平面ABB1A1,又DE?平面ABB1A1,
∴C1D1⊥DE,(8分)
取BB1的中点为P,连接AP、A1P,则AP∥DE,A1P∥D1F,
设AB=a,由AA1=2AB,BB1=4BE=4B1F,
在等腰直角△ABP和△A1B1P中,AP=
a,A1P=
a,
又AA1=2a,故AA12=AP2+A1P2,则AP⊥A1P,
∴在平面ABB1A1内,DE⊥D1F,(11分)
又C1D1∩D1F=D1,C1D1?平面C1D1F,FD1?平面C1D1F,
∴DE⊥平面C1D1F,又DE?平面DEG,
∴平面DEG⊥平面C1D1F.(14分)
 证明:(1)如图,取B1C1的中点H,连接GH、BH,
证明:(1)如图,取B1C1的中点H,连接GH、BH,∵D,G分别为AB,A1C1的中点,
∴GH∥A1B1,GH=
| 1 |
| 2 |
| 1 |
| 2 |
又三棱柱ABC-A1B1C1为正三棱柱,则BD∥GH,BD=GH,
故四边形BDGH为平行四边形,
∴DG∥BH,(4分)
又DG?平面BCC1B1,BH?平面BCC1B1,
∴DG∥平面BCC1B1;(6分)
(2)由三棱柱ABC-A1B1C1为正三棱柱,D1分别为A1B1的中点,
∴C1D1⊥平面ABB1A1,又DE?平面ABB1A1,
∴C1D1⊥DE,(8分)
取BB1的中点为P,连接AP、A1P,则AP∥DE,A1P∥D1F,
设AB=a,由AA1=2AB,BB1=4BE=4B1F,
在等腰直角△ABP和△A1B1P中,AP=
| 2 |
| 2 |
又AA1=2a,故AA12=AP2+A1P2,则AP⊥A1P,
∴在平面ABB1A1内,DE⊥D1F,(11分)
又C1D1∩D1F=D1,C1D1?平面C1D1F,FD1?平面C1D1F,
∴DE⊥平面C1D1F,又DE?平面DEG,
∴平面DEG⊥平面C1D1F.(14分)
点评:此题考查直线与平面平行的判断及平面与平面垂直的判断,此类问题一般先证明两个面平行,再证直线和面平行,这种做题思想要记住,此类立体几何题是每年高考必考的一道大题,同学们要课下要多练习.

练习册系列答案
相关题目
 如图,在正三棱柱ABC-A1B1C1中,AB=1,若二面角C-AB-C1的大小为60°,则点C到平面C1AB的距离为( )
如图,在正三棱柱ABC-A1B1C1中,AB=1,若二面角C-AB-C1的大小为60°,则点C到平面C1AB的距离为( )A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
 如图,在正三棱柱ABC-A1B1C1中,D、E、G分别是AB、BB1、AC1的中点,AB=BB1=2.
如图,在正三棱柱ABC-A1B1C1中,D、E、G分别是AB、BB1、AC1的中点,AB=BB1=2. 如图,在正三棱柱ABC-A1B1C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上,
如图,在正三棱柱ABC-A1B1C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上, (2012•马鞍山二模)如图,在正三棱柱ABC一DEF中,AB=2,AD=1,P是CF的延长线上一点,过A、B、P三点的平面交FD于M,交EF于N.
(2012•马鞍山二模)如图,在正三棱柱ABC一DEF中,AB=2,AD=1,P是CF的延长线上一点,过A、B、P三点的平面交FD于M,交EF于N.