题目内容
15.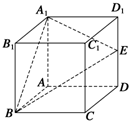 如图所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点.在棱C1D1上是否存在一点F,使B1F∥平面A1BE?证明你的结论.
如图所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点.在棱C1D1上是否存在一点F,使B1F∥平面A1BE?证明你的结论.
分析 分别取C1D1和CD的中点F,G,连接B1F,EG,BG,CD1,FG,由已知条件推导出四边形A1BCD1是平行四边形,进而各得到四边形B1BGF是平行四边形,由此能证明B1F∥平面A1BE.
解答 解:在棱C1D1上存在点F,使B1F∥平面A1BE.
证明如下:
如图所示,分别取C1D1和CD的中点F,G,连接B1F,EG,BG,CD1,FG.
∵A1D1∥B1C1∥BC,且A1D1=BC,
∴四边形A1BCD1是平行四边形,∴D1C∥A1B.
又E,G分别为D1D,CD的中点,∴EG∥D1C,
从而EG∥A1B.这说明A1,B,G,E四点共面,∴BG?平面A1BE.(6分)
∵四边形C1CDD1与B1BCC1都是正方形,F,G分别为C1D1和CD的中点,
∴FG∥C1C∥B1B,且FG=C1C=B1B,∴四边形B1BGF是平行四边形,
∴B1F∥BG.而B1F?平面A1BE,BG?平面A1BE,
∴B1F∥平面A1BE.(12分)
点评 本题考查使得线面平行的点是否存在的判断与证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
5.函数y=2log4(1-x)的图象大致是( )
| A. | 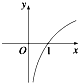 | B. | 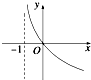 | C. | 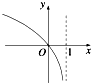 | D. | 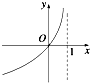 |
6.双曲线x2-4my2=4的实轴长是虚轴长的2倍,则实数m=( )
| A. | 1 | B. | $\frac{1}{16}$ | C. | $\frac{1}{2}$ | D. | 1或$\frac{1}{16}$ |
3.将圆x2+y2=1变换为椭圆$\frac{{{{x'}^2}}}{4}+\frac{{{{y'}^2}}}{9}=1$的伸缩变换公式为( )
| A. | $\left\{\begin{array}{l}x'=2x\\ y'=3y\end{array}\right.$ | B. | $\left\{\begin{array}{l}x'=3x\\ y'=2y\end{array}\right.$ | C. | $\left\{\begin{array}{l}x'=\frac{1}{2}x\\ y'=\frac{1}{3}y\end{array}\right.$ | D. | $\left\{\begin{array}{l}x'=\frac{1}{3}x\\ y'=\frac{1}{2}y\end{array}\right.$ |
10.有5本不同的语文书,4本不同的数学书,从中任意取出2本,那么下列各组中的两个事件是“互斥而不对立”是( )
| A. | “至少有一本是数学书”与“都是数学书” | |
| B. | “至少有一本是数学书”与“都是语文书” | |
| C. | “至少有一本是数学书”与“至少有1本是语文书” | |
| D. | “恰有1本是数学书”与“恰有2本是语文书” |
7.某几何体的三视图如图所示,则该几何体的体积为( )
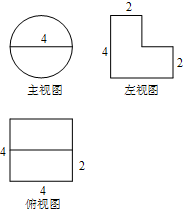

| A. | 4π | B. | 8π | C. | 12π | D. | 16π |
5.执行如图所示的程序框图,则输出的结果为( )
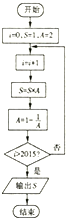

| A. | 2 | B. | 1 | C. | -1 | D. | -2 |