题目内容
已知F1,F2是椭圆 +
+ =1(a>b>0)的两个焦点,O为坐标原点,点P(-1,
=1(a>b>0)的两个焦点,O为坐标原点,点P(-1, )在椭圆上,且
)在椭圆上,且 •
• =0,⊙O是以F1F2为直径的圆,直线l:y=kx+m与⊙O相切,并且与椭圆交于不同的两点A,B
=0,⊙O是以F1F2为直径的圆,直线l:y=kx+m与⊙O相切,并且与椭圆交于不同的两点A,B(1)求椭圆的标准方程;
(2)当
 •
•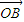 =λ,且满足
=λ,且满足 ≤λ≤
≤λ≤ 时,求弦长|AB|的取值范围.
时,求弦长|AB|的取值范围.
【答案】分析:(1)依题意,易得PF1⊥F1F2,进而可得c=1,根据椭圆的方程与性质可得 +
+ =1,a2=b2+c2,联立解可得a2、b2、c2的值,即可得答案;
=1,a2=b2+c2,联立解可得a2、b2、c2的值,即可得答案;
(2)根据题意,直线l与⊙x2+y2=1相切,则圆心到直线的距离等于圆的半径1,即 =1,变形为m2=k2+1,联立椭圆与直线的方程,即
=1,变形为m2=k2+1,联立椭圆与直线的方程,即 ,得(1+2k2)x2+4kmx+2m2-2=0,设由直线l与椭圆交于不同的两点A(x1,y1),B(x2,y2),则△>0,解可得k≠0,可得x1+x2=-
,得(1+2k2)x2+4kmx+2m2-2=0,设由直线l与椭圆交于不同的两点A(x1,y1),B(x2,y2),则△>0,解可得k≠0,可得x1+x2=- ,x1•x2=-
,x1•x2=- ,进而将其代入y1•y2=(kx1+m)(kx2+m)可得y1•y2关于k的表达式,又由
,进而将其代入y1•y2=(kx1+m)(kx2+m)可得y1•y2关于k的表达式,又由 =x1•x2+y1•y2=
=x1•x2+y1•y2= =
= ,结合题意
,结合题意 ≤λ≤
≤λ≤ ,解可得
,解可得 ≤k2≤1,根据弦长公式可得|AB|=2
≤k2≤1,根据弦长公式可得|AB|=2 ,设u=k4+k2(
,设u=k4+k2( ≤k2≤1),则
≤k2≤1),则 ≤u≤2,将|AB|用u表示出来,由u
≤u≤2,将|AB|用u表示出来,由u [
[ ,2]分析易得答案.
,2]分析易得答案.
解答:解:(1)依题意,由 •
• =0,可得PF1⊥F1F2,
=0,可得PF1⊥F1F2,
∴c=1,
将点p坐标代入椭圆方程可得 +
+ =1,又由a2=b2+c2,
=1,又由a2=b2+c2,
解得a2=2,b2=1,c2=1,
∴椭圆的方程为 +y2=1.
+y2=1.
(2)直线l:y=kx+m与⊙x2+y2=1相切,则 =1,即m2=k2+1,
=1,即m2=k2+1,
由直线l与椭圆交于不同的两点A、B,设A(x1,y1),B(x2,y2),
由 ,得(1+2k2)x2+4kmx+2m2-2=0,
,得(1+2k2)x2+4kmx+2m2-2=0,
△=(4km)2-4×(1+2k2)(2m2-2)>0,化简可得2k2>1+m2,
x1+x2=- ,x1•x2=-
,x1•x2=- ,
,
y1•y2=(kx1+m)(kx2+m)=k2x1•x2+km(x1+x2)+m2= =
= ,
,
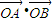 =x1•x2+y1•y2=
=x1•x2+y1•y2= =
= ,
,
 ≤
≤ ≤
≤ ,解可得
,解可得 ≤k2≤1,(9分)
≤k2≤1,(9分)
|AB|=
 =2
=2
设u=k4+k2( ≤k2≤1),
≤k2≤1),
则 ≤u≤2,|AB|=2
≤u≤2,|AB|=2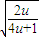 =2
=2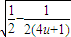 ,u
,u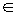 [
[ ,2]
,2]
分析易得, ≤|AB|≤
≤|AB|≤ .(13分)
.(13分)
点评:本题考查直线与椭圆的位置关系,解此类题目,一般要联系直线与圆锥曲线的方程,得到一元二次方程,利用根与系数的关系来求解.
 +
+ =1,a2=b2+c2,联立解可得a2、b2、c2的值,即可得答案;
=1,a2=b2+c2,联立解可得a2、b2、c2的值,即可得答案;(2)根据题意,直线l与⊙x2+y2=1相切,则圆心到直线的距离等于圆的半径1,即
 =1,变形为m2=k2+1,联立椭圆与直线的方程,即
=1,变形为m2=k2+1,联立椭圆与直线的方程,即 ,得(1+2k2)x2+4kmx+2m2-2=0,设由直线l与椭圆交于不同的两点A(x1,y1),B(x2,y2),则△>0,解可得k≠0,可得x1+x2=-
,得(1+2k2)x2+4kmx+2m2-2=0,设由直线l与椭圆交于不同的两点A(x1,y1),B(x2,y2),则△>0,解可得k≠0,可得x1+x2=- ,x1•x2=-
,x1•x2=- ,进而将其代入y1•y2=(kx1+m)(kx2+m)可得y1•y2关于k的表达式,又由
,进而将其代入y1•y2=(kx1+m)(kx2+m)可得y1•y2关于k的表达式,又由 =x1•x2+y1•y2=
=x1•x2+y1•y2= =
= ,结合题意
,结合题意 ≤λ≤
≤λ≤ ,解可得
,解可得 ≤k2≤1,根据弦长公式可得|AB|=2
≤k2≤1,根据弦长公式可得|AB|=2 ,设u=k4+k2(
,设u=k4+k2( ≤k2≤1),则
≤k2≤1),则 ≤u≤2,将|AB|用u表示出来,由u
≤u≤2,将|AB|用u表示出来,由u [
[ ,2]分析易得答案.
,2]分析易得答案.解答:解:(1)依题意,由
 •
• =0,可得PF1⊥F1F2,
=0,可得PF1⊥F1F2,∴c=1,
将点p坐标代入椭圆方程可得
 +
+ =1,又由a2=b2+c2,
=1,又由a2=b2+c2,解得a2=2,b2=1,c2=1,
∴椭圆的方程为
 +y2=1.
+y2=1.(2)直线l:y=kx+m与⊙x2+y2=1相切,则
 =1,即m2=k2+1,
=1,即m2=k2+1,由直线l与椭圆交于不同的两点A、B,设A(x1,y1),B(x2,y2),
由
 ,得(1+2k2)x2+4kmx+2m2-2=0,
,得(1+2k2)x2+4kmx+2m2-2=0,△=(4km)2-4×(1+2k2)(2m2-2)>0,化简可得2k2>1+m2,
x1+x2=-
 ,x1•x2=-
,x1•x2=- ,
,y1•y2=(kx1+m)(kx2+m)=k2x1•x2+km(x1+x2)+m2=
 =
= ,
,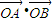 =x1•x2+y1•y2=
=x1•x2+y1•y2= =
= ,
, ≤
≤ ≤
≤ ,解可得
,解可得 ≤k2≤1,(9分)
≤k2≤1,(9分)|AB|=

 =2
=2
设u=k4+k2(
 ≤k2≤1),
≤k2≤1),则
 ≤u≤2,|AB|=2
≤u≤2,|AB|=2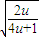 =2
=2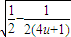 ,u
,u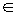 [
[ ,2]
,2]分析易得,
 ≤|AB|≤
≤|AB|≤ .(13分)
.(13分)点评:本题考查直线与椭圆的位置关系,解此类题目,一般要联系直线与圆锥曲线的方程,得到一元二次方程,利用根与系数的关系来求解.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目