题目内容
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() ,椭圆
,椭圆![]() 的右顶点为
的右顶点为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知纵坐标不同的两点![]() ,
,![]() 为椭圆
为椭圆![]() 上的两个点,且
上的两个点,且![]() ,
,![]() ,
,![]() 三点共线,线段
三点共线,线段![]() 的中点为
的中点为![]() ,求直线
,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由题意结合椭圆的性质可得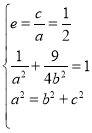 ,求得
,求得![]() 、
、![]() 即可得解;
即可得解;
(2)由题意设直线![]() 方程为
方程为![]() ,点
,点![]() ,
,![]() ,
,![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,联立方程结合韦达定理可表示出点
,联立方程结合韦达定理可表示出点![]() 的坐标,进而可得
的坐标,进而可得![]() ,结合基本不等式即可得解.
,结合基本不等式即可得解.
(1)∵椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() ,
,
∴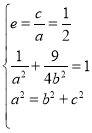 ,解得
,解得![]() ,
,![]() ,
,
∴椭圆![]() 的方程为
的方程为![]() ;
;
(2)依题意知直线![]() 过点
过点![]() ,且斜率不为0,
,且斜率不为0,
故可设其方程为![]() ,
,
由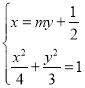 ,消去
,消去![]() 得
得![]() ,
,![]() ,
,
设点![]() ,
,![]() ,
,![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,
,
故![]() ,∴
,∴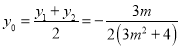 ,∴
,∴![]() ,
,
又点![]() 的坐标为
的坐标为![]() ,∴
,∴![]() ,
,
当![]() 时,
时,![]() ;
;
当![]() 时,
时,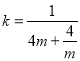 ,
,
∵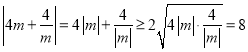 ,当且仅当
,当且仅当![]() 时,等号成立,
时,等号成立,
∴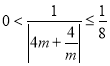 ,∴
,∴![]() ,
,
∴![]() 且
且![]() ;
;
综上所述,直线![]() 的斜率的取值范围是
的斜率的取值范围是![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某科研课题组通过一款手机APP软件,调查了某市1000名跑步爱好者平均每周的跑步量(简称“周跑量”),得到如下的频数分布表
周跑量(km/周) |
|
|
|
|
|
|
|
|
|
人数 | 100 | 120 | 130 | 180 | 220 | 150 | 60 | 30 | 10 |
(1)在答题卡上补全该市1000名跑步爱好者周跑量的频率分布直方图:

注:请先用铅笔画,确定后再用黑色水笔描黑
(2)根据以上图表数据计算得样本的平均数为![]() ,试求样本的中位数(保留一位小数),并用平均数、中位数等数字特征估计该市跑步爱好者周跑量的分布特点
,试求样本的中位数(保留一位小数),并用平均数、中位数等数字特征估计该市跑步爱好者周跑量的分布特点
(3)根据跑步爱好者的周跑量,将跑步爱好者分成以下三类,不同类别的跑者购买的装备的价格不一样,如下表:
周跑量 | 小于20公里 | 20公里到40公里 | 不小于40公里 |
类别 | 休闲跑者 | 核心跑者 | 精英跑者 |
装备价格(单位:元) | 2500 | 4000 | 4500 |
根据以上数据,估计该市每位跑步爱好者购买装备,平均需要花费多少元?