题目内容
【题目】如图,等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 中点,以
中点,以![]() 为折痕把
为折痕把![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置(
的位置(![]() 平面
平面![]() ).
).

(1)证明:![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接![]() ,设
,设![]() 的中点为
的中点为![]() ,可证
,可证![]() ,
,![]() ,由线面垂直的判定定理可知
,由线面垂直的判定定理可知![]() 平面
平面![]() ,于是即可证明
,于是即可证明![]() ;
;
(2)由勾股定理可证![]() ,建立空间坐标系,求出两半平面的法向量,计算法向量的夹角,由此即可求出二面角的大小.
,建立空间坐标系,求出两半平面的法向量,计算法向量的夹角,由此即可求出二面角的大小.
(1)连接![]() ,
,
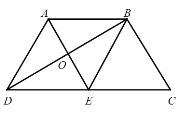
设![]() 的中点为
的中点为![]() ,
,
∵![]() ,
,![]() ,
,
∴四边形![]() 为平行四边形,∴
为平行四边形,∴![]() ,
,
∴![]() ,
,![]() 为等边三角形,
为等边三角形,
∴![]() ,
,![]() ,折叠后
,折叠后![]() ,
,![]() ,
,
又![]() ,∴
,∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,∴
,∴![]() .
.
(2)由已知得![]() ,
,
又![]() ,∴
,∴![]() ,
,![]() ,
,
又![]() ,
,![]() ,则
,则![]() 平面
平面![]() ,
,
以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,

则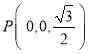 ,
,![]() ,
,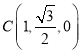 ,
,
∴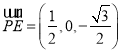 ,
,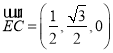 ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则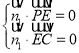 ,即
,即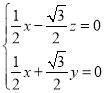 ,
,
令![]() 得
得![]() ,
,
又![]() 平面
平面![]() ,∴
,∴![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
设二面角![]() 为
为![]() ,则
,则 ,
,
由图可知二面角![]() 为钝角,所以
为钝角,所以![]() .
.

练习册系列答案
相关题目
【题目】上世纪末河南出土的以鹤的尺骨(翅骨)制成的“骨笛”(图1),充分展示了我国古代高超的音律艺术及先进的数学水平,也印证了我国古代音律与历法的密切联系.图2为骨笛测量“春(秋)分”,“夏(冬)至”的示意图,图3是某骨笛的部分测量数据(骨笛的弯曲忽略不计),夏至(或冬至)日光(当日正午太阳光线)与春秋分日光(当日正午太阳光线)的夹角等于黄赤交角.

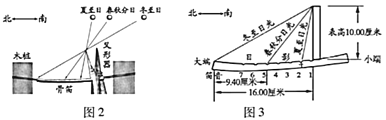
由历法理论知,黄赤交角近1万年持续减小,其正切值及对应的年代如下表:
黄赤交角 |
|
|
|
|
|
正切值 | 0.439 | 0.444 | 0.450 | 0.455 | 0.461 |
年代 | 公元元年 | 公元前2000年 | 公元前4000年 | 公元前6000年 | 公元前8000年 |
根据以上信息,通过计算黄赤交角,可估计该骨笛的大致年代是( )
A.公元前2000年到公元元年B.公元前4000年到公元前2000年
C.公元前6000年到公元前4000年D.早于公元前6000年

