题目内容
【题目】已知![]() 是双曲线
是双曲线![]() 的左右焦点,以
的左右焦点,以![]() 为直径的圆与双曲线的一条渐近线交于点
为直径的圆与双曲线的一条渐近线交于点![]() ,与双曲线交于点
,与双曲线交于点![]() ,且
,且![]() 均在第一象限,当直线
均在第一象限,当直线![]() 时,双曲线的离心率为
时,双曲线的离心率为![]() ,若函数
,若函数![]() ,则
,则![]() ()
()
A. 1 B. ![]() C. 2 D.
C. 2 D. ![]()
【答案】C
【解析】双曲线的![]() ,双曲线的渐近线方程为
,双曲线的渐近线方程为![]() 与圆
与圆![]() 联立,解得
联立,解得![]() ,与双曲线方程
,与双曲线方程![]() 联立,解得
联立,解得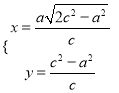 ,即为
,即为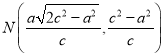 ,直线
,直线![]() 与直线
与直线![]() 平行时,既有
平行时,既有![]() ,即
,即![]() ,既有
,既有![]() ,
, ![]() ,即
,即![]()
![]() ,故选C.
,故选C.
【方法点晴】本题主要考查利用双曲线的简单性质求双曲线的离心率、双曲线的渐近线,属于难题. 求解与双曲线性质有关的问题时要结合图形进行分析,既使不画出图形,思考时也要联想到图形,当涉及顶点、焦点、实轴、虚轴、渐近线等双曲线的基本量时,要理清它们之间的关系,挖掘出它们之间的内在联系.求与离心率有关的问题,应先将![]() 用有关的一些量表示出来,再利用其中的一些关系构造出关于e的等式.
用有关的一些量表示出来,再利用其中的一些关系构造出关于e的等式.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目