题目内容
(2012•鹰潭模拟)如图,在边长为4的菱形ABCD中,∠DAB=60°.点E、F分别在边CD、CB上,点E与点C、D不重合,EF⊥AC,EF∩AC=O.沿EF将△CEF翻折到△PEF的位置,使平面PEF⊥平面ABFED.
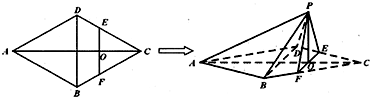
(1)求证:BD⊥平面POA;
(2)当PB取得最小值时,求四棱锥P-BDEF的体积.

(1)求证:BD⊥平面POA;
(2)当PB取得最小值时,求四棱锥P-BDEF的体积.
分析:(1)由菱形ABCD的对角线互相垂直,知BD⊥AC,BD⊥AO,由EF⊥AC,知PO⊥EF.由此能够证明BD⊥平面POA.
(2)设AO∩BD=H.因为∠DAB=60°,所以△BDC为等边三角形,故BD=4,HB=2, HC=2
.由此入手能够求出当PB取得最小值时四棱锥P-BDEF的体积.
(2)设AO∩BD=H.因为∠DAB=60°,所以△BDC为等边三角形,故BD=4,HB=2, HC=2
| 3 |
解答:解:(1)证明:∵菱形ABCD的对角线互相垂直,
∴BD⊥AC,∴BD⊥AO,
∵EF⊥AC,∴PO⊥EF.
∵平面PEF⊥平面ABFED,平面PEF∩平面ABFED=EF,且PO?平面PEF,
∴PO⊥平面ABFED,
∵BD?平面ABFED,∴PO⊥BD.
∵AO∩PO=O,∴BD⊥平面POA.…(4分)
(2)设AO∩BD=H.因为∠DAB=60°,
所以△BDC为等边三角形,
故BD=4,HB=2, HC=2
.
又设PO=x,则OH=2
-x,OA=4
-x.
由OH⊥BD,则|OB|2=(2
-x)2+22,
又由(1)知,PO⊥平面BFED,则PO⊥OB
所以|PB|=
=
,
当x=
时,|PB|min=
.
此时PO=
,…(8分)
所以V四棱锥P-BFED=
•S梯形BFED•PO=
•(
×42-
×22)×
=3.…(12分)
∴BD⊥AC,∴BD⊥AO,
∵EF⊥AC,∴PO⊥EF.
∵平面PEF⊥平面ABFED,平面PEF∩平面ABFED=EF,且PO?平面PEF,
∴PO⊥平面ABFED,
∵BD?平面ABFED,∴PO⊥BD.
∵AO∩PO=O,∴BD⊥平面POA.…(4分)
(2)设AO∩BD=H.因为∠DAB=60°,
所以△BDC为等边三角形,
故BD=4,HB=2, HC=2
| 3 |
又设PO=x,则OH=2
| 3 |
| 3 |
由OH⊥BD,则|OB|2=(2
| 3 |
又由(1)知,PO⊥平面BFED,则PO⊥OB
所以|PB|=
(2
|
2(x-
|
当x=
| 3 |
| 10 |
此时PO=
| 3 |
所以V四棱锥P-BFED=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 4 |
| ||
| 4 |
| 3 |
点评:本题考查直线与平面垂直的证明,考查四锥锥体积的求法.解题时要认真审题,仔细解答,注意合理地化空间问题为平面问题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目