题目内容
(本小题满分16分)
已知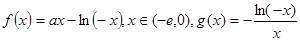 ,其中
,其中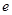 是自然常数,
是自然常数,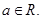
(1)讨论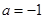 时,
时, 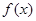 的单调性、极值;
的单调性、极值;
(2)求证:在(1)的条件下, ;
;
(3)是否存在实数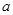 ,使
,使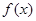 的最小值是3,如果存在,求出
的最小值是3,如果存在,求出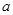 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
【答案】
(1)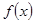 的极小值为
的极小值为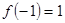 ;
;
(2)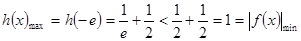 ,
,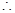 当
当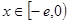 时,
时,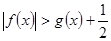 ;
;
(3)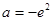 。
。
【解析】(I)当a=1时,f(x)的解析式确定,然后利用导数研究其单调性、极值即可.
(2)在(1)条件下,可确定出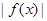 的最小值,然后再利用导数研究
的最小值,然后再利用导数研究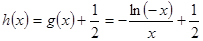 的最大值即可.只需证明
的最大值即可.只需证明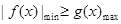 即可.
即可.
(3)先假设存在实数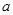 ,使
,使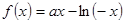 有最小值3,
有最小值3,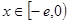 ,
,
然后求出f(x)的导数,利用其导数研究其最小值,根据最小值等于3,求a,看a值是否存在.
(1)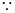

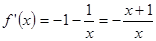 ------------2分
------------2分
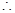 当
当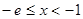 时,
时,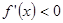 ,此时
,此时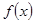 为单调递减
为单调递减
当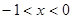 时,
时,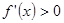 ,此时
,此时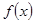 为单调递增
为单调递增
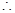
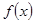 的极小值为
的极小值为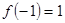 --------------------------4分
--------------------------4分
(2)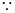
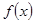 的极小值,即
的极小值,即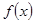 在
在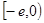 的最小值为1
的最小值为1
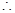
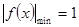 令
令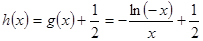
又
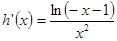 ------------------------6分
------------------------6分
当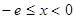 时
时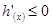
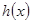 在
在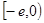 上单调递减
上单调递减
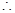
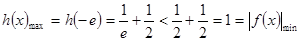 ---------------7分
---------------7分
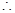 当
当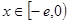 时,
时,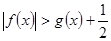 ------------------------------8分
------------------------------8分
(3)假设存在实数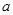 ,使
,使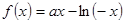 有最小值3,
有最小值3,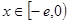
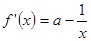
①当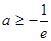 时,由于
时,由于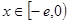 ,则
,则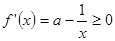
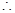 函数
函数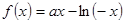 是
是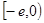 上的增函数
上的增函数
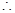
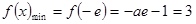
解得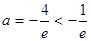 (舍去) ---------------------------------12分
(舍去) ---------------------------------12分
②当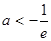 时,则当
时,则当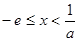 时,
时,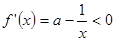
此时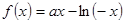 是减函数
是减函数
当 时,
时,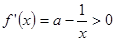 ,此时
,此时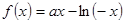 是增函数
是增函数
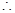
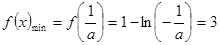
解得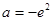 ---------------------------------16分
---------------------------------16分

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 在平面直角坐标系
在平面直角坐标系 ,
, (
( ),
),
 ,对任意
,对任意 时,
时, 恒成立,求实数
恒成立,求实数 的范围;
的范围; ,当“
,当“ 在
在 的最大值.
的最大值. :方程
:方程 无实数根;
命题
无实数根;
命题 :函数
:函数 的值域是
的值域是 .如果命题
.如果命题 为真命题,
为真命题, 为假命题,求实数
为假命题,求实数 的取值范围.
的取值范围. 为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
 )的值;
)的值; 个单位后,再将得到的图象上各点的横坐标延长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标延长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.