Question

已知函数f(x)＝ae^x，g(x)＝lnx－lna，其中a为常数， e＝2.718…，且函数y＝f(x)和y＝g(x)的图像在它们与坐标轴交点处的切线互相平行．

(1)求常数a的值；

(2)若存在x使不等式>成立，求实数m的取值范围；

(3)对于函数y＝f(x)和y＝g(x)公共定义域内的任意实数x₀，我们把|f(x₀)－g(x₀)|的值称为两函数在x₀处的偏差．求证：函数y＝f(x)和y＝g(x)在其公共定义域内的所有偏差都大于2.

 

Answer 1

【答案】

（1）；（2）；（3）参考解析

【解析】

试题分析：（1）依题意可得函数与坐标轴的交点通过求导函数即在两坐标轴的交点的切线的斜率相等即可求出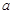的值.

（2）不等式恒成立的问题转化为函数的最值问题.在对函数求导求出在定义域上的单调性即可求出m的取值范围.

（3）本小题是把不等式的问题转化为一个新的函数的最问题. 由于.对该函数直接研究存在困难.求导后不能得到所需要的结论.所以构造新函数从而得到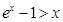.再构造一个函数得到lnx+1<x.从而得到偏差要大于2的结论.本小题的解法较特殊.构造两个函数额是解题的关键和突破口，同时既有创新思维.

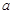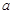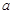试题解析：（1）f(x)与坐标轴的交点为(0,). . g(x)与坐标轴的交点为(,0). .所以.所以.又因为>0.所以.

（2）因为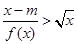可化为.令.则.因为x>0.所以..所以.故.所以在上是减函数.因此.所以实数m的取值范围是.

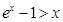（3）y=f(x)与y=g(x)的公共定义域为..令.则>0.所以h(x)在上是增函数.故h(x)>h(0)=0.即…①.令.则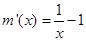.当x>1.时. .当0<x<1时. .所以m(x)有最大值m(1)=0.因此lnx+1<x…②.由①②得.即.所以函数y=f(x)和y=g(x)在其公共定义域内的所有偏差都大于2.

考点：1.导数的几何意义.2.不等式转化为恒成立问题.3.函数的构造.