题目内容
（2012•乐山二模）已知△ABC的三个顶点在同一个球面上，∠BAC=60°，AB=1，AC=2，若球心到平面ABC的距离为1，则该球的体积为（ ）
分析：由“∠BAC=60°，AB=1，AC=2，”得到AB即为A、B、C三点所在圆的直径，取AB的中点M，连接OM，则OM即为球心到平面ABC的距离，在Rt△OMB中，OM=1，MB=1，则OB可求，从而得出该球的体积．
解答：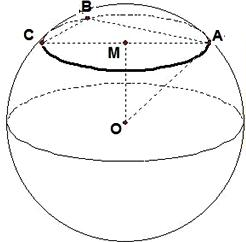
解：在三角形ABC中，∠BAC=60°，AB=1，AC=2，∴BC=
，
则三角形ABC是以AC为斜边的直角三角形，
如图所示：
取AC的中点M，则球面上A、B、C三点所在的圆即为⊙M，连接OM，则OM即为球心到平面ABC的距离，
在Rt△OMB中，OM=1，MA=1，
∴OA=
，即球球的半径为
．
所以球的体积为：
π×(
)3=
．
故选D．
解：在三角形ABC中，∠BAC=60°，AB=1，AC=2，∴BC=| 3 |
则三角形ABC是以AC为斜边的直角三角形，
如图所示：
取AC的中点M，则球面上A、B、C三点所在的圆即为⊙M，连接OM，则OM即为球心到平面ABC的距离，
在Rt△OMB中，OM=1，MA=1，
∴OA=
| 2 |
| 2 |
所以球的体积为：
| 4 |
| 3 |
| 2 |
8
| ||
| 3 |
故选D．
点评：本题考查球的有关计算问题，点到平面的距离，是基础题．
练习册系列答案
相关题目
（2012•乐山二模）一个频率分布表（样本容量为30）不小心被损坏了一部分（如图），只记得样本中数据在[20，60）上的频率为0.8，则估计样本在[40，50），[50，60）内的数据个数可能是（ ）
（2012•乐山二模）如图，球O夹在锐二面角α-l-β之间，与两个半平面的切点分别为A、B，若AB=