题目内容
(2012•乐山二模)对于非空集合A、B,定义运算A⊕B={x|x∈A∪B,且x∉A∩B.已知两个开区间M=(a,b),N=(c,d),其中a、b、c、d满足a+b<c+d,ab=cd<0,则M⊕N=( )
分析:根据已知的a+b<c+d,ab=cd<0,且区间左端点小于右端点,得出a,b,c,d的大小关系,在数轴上画出两个区间,根据题意的新定义A+B,即可求出M+N.
解答:解:∵a+b<c+d,ab=cd<0,且a<b,c<d,
∴a<c<0<b<d,
把两区间表示在数轴上,如图所示:
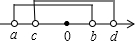
∴M∪N=(a,d),M∩N=(c,d),
则M+N=(a,c)∪(b,d).
故选B
∴a<c<0<b<d,
把两区间表示在数轴上,如图所示:

∴M∪N=(a,d),M∩N=(c,d),
则M+N=(a,c)∪(b,d).
故选B
点评:此题考查了交集、并集的运算,利用了转化及数形结合的思想,其中根据题意得出字母的大小关系,理解掌握新定义是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•乐山二模)一个频率分布表(样本容量为30)不小心被损坏了一部分(如图),只记得样本中数据在[20,60)上的频率为0.8,则估计样本在[40,50),[50,60)内的数据个数可能是( )
(2012•乐山二模)一个频率分布表(样本容量为30)不小心被损坏了一部分(如图),只记得样本中数据在[20,60)上的频率为0.8,则估计样本在[40,50),[50,60)内的数据个数可能是( ) (2012•乐山二模)如图,球O夹在锐二面角α-l-β之间,与两个半平面的切点分别为A、B,若AB=
(2012•乐山二模)如图,球O夹在锐二面角α-l-β之间,与两个半平面的切点分别为A、B,若AB=