题目内容
(本小题满分12分)
如图,四棱锥 中,底面
中,底面 为矩形,
为矩形, 平面
平面 ,点
,点 分别是
分别是 和
和 的中点.
的中点.

求证: 平面
平面 ;
;
若 , 四棱锥
, 四棱锥 外接球的表面积.
外接球的表面积.
如图,四棱锥
 中,底面
中,底面 为矩形,
为矩形, 平面
平面 ,点
,点 分别是
分别是 和
和 的中点.
的中点.
求证:
 平面
平面 ;
;若
 , 四棱锥
, 四棱锥 外接球的表面积.
外接球的表面积.(1)取PD的中点G,连接FG,GA,GF//DC,GF= DC,AE=
DC,AE= AB,矩形ABCD中,AB//DC,AB=DC,∴GF//AE,GF=AE?∴四边形AEFG是平行四边形,EF//AG,EF在平面PDA外,AG在平面PDA内,
AB,矩形ABCD中,AB//DC,AB=DC,∴GF//AE,GF=AE?∴四边形AEFG是平行四边形,EF//AG,EF在平面PDA外,AG在平面PDA内,
∴EF//平面PDA.(2)6
 DC,AE=
DC,AE= AB,矩形ABCD中,AB//DC,AB=DC,∴GF//AE,GF=AE?∴四边形AEFG是平行四边形,EF//AG,EF在平面PDA外,AG在平面PDA内,
AB,矩形ABCD中,AB//DC,AB=DC,∴GF//AE,GF=AE?∴四边形AEFG是平行四边形,EF//AG,EF在平面PDA外,AG在平面PDA内,∴EF//平面PDA.(2)6

试题分析:(1)取PD的中点G,连接FG,GA,由G、F分别是PD、PC的中点,知GF是△PDC的中位线,
GF//DC,GF=
 DC,
DC,E是AB中点,AE=
 AB,
AB,矩形ABCD中,AB//DC,AB=DC,
∴GF//AE,GF=AE? ……………………3分
∴四边形AEFG是平行四边形,EF//AG,
EF在平面PDA外,AG在平面PDA内,
∴EF//平面PDA. ……………………6分
(2)由图易知AB⊥平面PAD,四棱锥P-ABCD的 外接球即以DP,DA,DC为棱的长方体的外接球。
∴R=
 ,∴S=4
,∴S=4 =6
=6 。 ……………………12分
。 ……………………12分点评:本题在证明线面平行时充分利用已知中出现的中点作出三角形中位线即可实现直线间的平行,此三棱锥是长方体一部分,其外接球转化为长方体外接球求解较容易

练习册系列答案
相关题目




 ,
, ,
, 组成的支架,三根铁杆的两两夹角都是
组成的支架,三根铁杆的两两夹角都是 ,一个半径为1的球放在支架上,则球心到
,一个半径为1的球放在支架上,则球心到 的距离为____________
的距离为____________
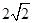 的等腰三角形,俯视图是边长为4的正方形,则这个几何体的表面积是__________
的等腰三角形,俯视图是边长为4的正方形,则这个几何体的表面积是__________






