题目内容
如下图所示,将平面四边形ABCD折成空间四边形,当平面四边形满足条件 时,空间四边形中的两条对角线互相垂直(填一个正确答案就可以,不必考虑所有可能情形)




试题分析:在平面四边形中,设AC与BD交于E,假设AC⊥BD,则AC⊥DE,AC⊥BE.折叠后,AC与DE,AC与BE依然垂直,所以AC⊥平面BDE.所以AC⊥BD.
若四边形ABCD为菱形或正方形,因为它们的对角线互相垂直,仿上可证AC⊥BD.
故答案可为AC⊥BD(或ABCD为菱形,正方形等.).
点评:简单题,这是一道开放式题目,其正确答案可能不止一个,写出一个即可。折叠问题,要特别注意折叠前后变与不变 的几何运算。

练习册系列答案
相关题目

 π
π

 中,底面
中,底面 为矩形,
为矩形, 平面
平面 分别是
分别是 和
和 的中点.
的中点.
 平面
平面 ;
; , 四棱锥
, 四棱锥 在空间直角坐标系中移动,但保持点A、B分别在x轴、y轴上移动,则点
在空间直角坐标系中移动,但保持点A、B分别在x轴、y轴上移动,则点 到原点O的最远距离为( )
到原点O的最远距离为( ) B.
B.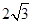 C.5 D.4
C.5 D.4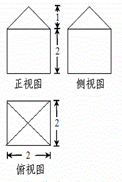






 ,侧棱长是3,点E、F分别在BB1、DD1上,且AE⊥A1B,AF⊥A1D.
,侧棱长是3,点E、F分别在BB1、DD1上,且AE⊥A1B,AF⊥A1D.
 的正切值.
的正切值.