题目内容
商场销售某一品牌的羊毛衫,购买人数是羊毛衫标价的一次函数,标价越高,购买人数越少.把购买人数为零时的最低标价称为无效价格,已知无效价格为每件300元.现在这种羊毛衫的成本价是100元/ 件,商场以高于成本价的价格(标价)出售. 问:
(1)商场要获取最大利润,羊毛衫的标价应定为每件多少元?
(2)通常情况下,获取最大利润只是一种“理想结果”,如果商场要获得最大利润的75%,那么羊毛衫的标价为每件多少元?
(1)标价应定为每件200元(2)每件标价为250元或150元
解析试题分析:(1)设购买人数为n人,羊毛衫的标价为每件x元,利润为y元,则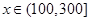 ,
,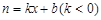 ,∵
,∵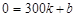 ,即
,即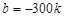 ,∴
,∴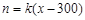 ,
,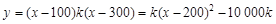 (x∈(100,300]),
(x∈(100,300]),
∵k<0,∴x = 200时,ymax =-10 000k,
即商场要获取最大利润,羊毛衫的标价应定为每件200元. ……8分
(2)由题意得,k(x-100)(x-300) =-10 000k·75%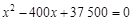
解得x = 250或x = 150,
所以,商场要获取最大利润的75%,每件标价为250元或150元. ……14分
考点:本小题主要考二次函数在实际问题中的应用.
点评:用函数解决实际问题时,首先要根据题意选择合适的函数模型,将实际问题转化为数学问题
解决,并且要注意实际问题中的定义域.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
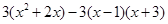
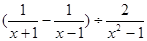
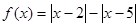 .
.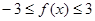 ;
;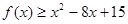 的解集.
的解集.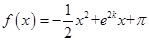 在
在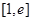 上具有单调性,求实数
上具有单调性,求实数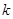 的取值范围;
的取值范围; 、
、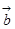 、
、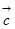 两两所成的角相等,且
两两所成的角相等,且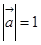 ,
,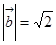 ,
,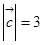 ,求
,求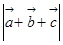 .
.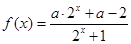
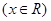 ,若
,若 满足
满足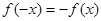 ,
, 的值; (2)判断函数的单调性,并加以证明。
的值; (2)判断函数的单调性,并加以证明。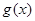 与
与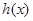 大小, 并写出完成总任务的时间
大小, 并写出完成总任务的时间 的表达式;
的表达式; ,
,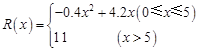 ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题: )
)