题目内容
(本小题满分12分)
(Ⅰ)已知函数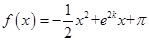 在
在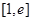 上具有单调性,求实数
上具有单调性,求实数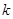 的取值范围;
的取值范围;
(Ⅱ)已知向量 、
、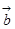 、
、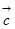 两两所成的角相等,且
两两所成的角相等,且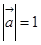 ,
,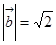 ,
,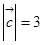 ,求
,求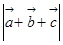 .
.
(Ⅰ)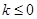 或
或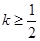 (Ⅱ)
(Ⅱ)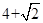 或
或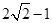
解析试题分析:(Ⅰ)因为函数 是二次函数,其图象对称轴为
是二次函数,其图象对称轴为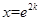
又 在
在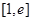 上具有单调性,
上具有单调性,
所以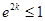 或
或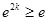 ,
,
解得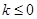 或
或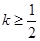 ,
,
故实数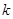 的取值范围是
的取值范围是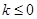 或
或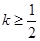 .
.
(Ⅱ)当 向量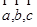 两两所成的角为
两两所成的角为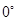 时,
时,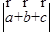 =
=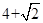
当 向量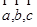 两两所成的角为
两两所成的角为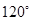 时,
时,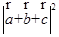 =
=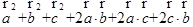
=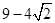
所以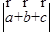 =
=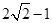
故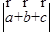 =
=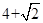 或
或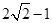
考点:二次函数的性质 向量运算
点评:第一问中考查二次函数的性质和应用,是基础题.解题的关键是灵活应用二次函数的性质,第二问中主要把握好向量模和数量积间的转化.

练习册系列答案
相关题目

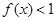 的解集为
的解集为 ,求
,求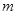 的取值范围;
的取值范围; 的不等式
的不等式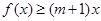 ;
;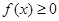 对一切
对一切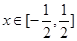 恒成立,求
恒成立,求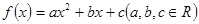 满足下列条件:①当
满足下列条件:①当 时,
时, 的最小值为
的最小值为 ,且图像关于直线
,且图像关于直线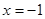 对称;②当
对称;②当 时,
时, 恒成立.
恒成立.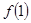 的值;
的值;  的解析式;
的解析式; 上恒有
上恒有 ,求实数
,求实数 的取值范围.
的取值范围.
 个月的旅游人数的和
个月的旅游人数的和 (单位:万人)与
(单位:万人)与 已知第
已知第 (单位:元)与
(单位:元)与
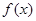 (单位:万人)与x的函数关系式;
(单位:万人)与x的函数关系式; (如图),考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为
(如图),考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为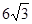 平方米,为了使堤的上面与两侧面的水泥用料最省,则断面的外周长(梯形的上底线段
平方米,为了使堤的上面与两侧面的水泥用料最省,则断面的外周长(梯形的上底线段 与两腰长的和)要最小.
与两腰长的和)要最小.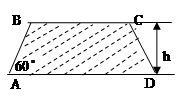
 的范围内,外周长最小为多少米?
的范围内,外周长最小为多少米?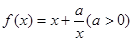 .
. 在定义域上的单调性;
在定义域上的单调性;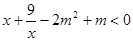 在
在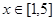 上恒成立时的实数
上恒成立时的实数 的取值范围?
的取值范围?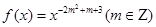 为偶函数,且在
为偶函数,且在 上为增函数.
上为增函数. 的值,并确定
的值,并确定 的解析式;
的解析式; 且
且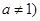 ,是否存在实数
,是否存在实数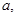 使
使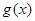 在区间
在区间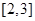 上的最大值为2,若存在,求出
上的最大值为2,若存在,求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.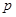 (万元)和
(万元)和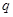 (万元),它们与投入的资金
(万元),它们与投入的资金 (万元)的关系,据经验估计为:
(万元)的关系,据经验估计为: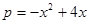 ,
, 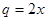 今有3万元资金投入经销甲、乙两种商品,为了获得最大利润,应对甲、乙两种商品分别投入多少资金?总共获得的最大利润是多少万元?
今有3万元资金投入经销甲、乙两种商品,为了获得最大利润,应对甲、乙两种商品分别投入多少资金?总共获得的最大利润是多少万元?