题目内容
【题目】微信运动和运动手环的普及,增强了人民运动的积极性,每天一万步称为一种健康时尚,某中学在全校范围内内积极倡导和督促师生开展“每天一万步”活动,经过几个月的扎实落地工作后,学校想了解全校师生每天一万步的情况,学校界定一人一天走路不足4千步为不健康生活方式,不少于16千步为超健康生活方式者,其他为一般生活方式者,学校委托数学组调查,数学组采用分层抽样的办法去估计全校师生的情况,结合实际及便于分层抽样,认定全校教师人数为200人,高一学生人数为700人,高二学生人数600人,高三学生人数500,从中抽取n人作为调查对象,得到了如图所示的这n人的频率分布直方图,这n人中有20人被学校界定为不健康生活方式者. 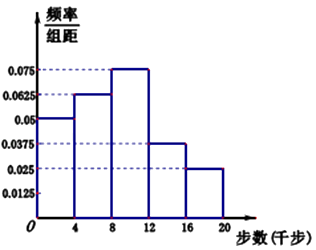
(1)求这次作为抽样调查对象的教师人数;
(2)根据频率分布直方图估算全校师生每人一天走路步数的中位数(四舍五入精确到整数步);
(3)校办公室欲从全校师生中速记抽取3人作为“每天一万步”活动的慰问对象,计划学校界定不健康生活方式者鞭策性精神鼓励0元,超健康生活方式者表彰奖励20元,一般生活方式者鼓励性奖励10元,利用样本估计总体,将频率视为概率,求这次校办公室慰问奖励金额X的分布列和数学期望.
【答案】
(1)解:由频率分布直方图知[0,4)的频率为0.05×4=0.2,于是 ![]() ,
,
由分层抽样的原理知这次作为抽样调查对象的教师人数为 ![]() 人.
人.
(2)解:由频率分布直方图知[0,4)的频率为0.2,[4,8)的频率为0.25,[8,12)的频率为0.3,
设中位数为x,则0.2+0.25+(x﹣8)×0.075=0.5,于是 ![]() (千步);
(千步);
(3)解:有频率分布直方图知不健康生活方式者概率为0.2,超健康生活方式者的概率为0.1,
一般生活方式者的概率为0.7,0≤X≤60,X的可能取值为0,10,20,30,40,50,60,
则 ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
P(X=60)=0.13=0.001.
X | 0 | 10 | 20 | 30 | 40 | 50 | 60 |
P | 0.008 | 0.084 | 0.306 | 0.427 | 0.153 | 0.021 | 0.001 |
E(X)=0×0.008+10×0.084+20×0.306+30×0.427+40×0.153+50×0.021+60×0.001=27(元)
所以这次校办公室慰问奖励金额X的数学期望为27元.
【解析】(1)利用频率分布直方图的性质与分层抽样的原理即可得出.(2)利用频率分布直方图的性质与中位数的定义即可得出.(3)有频率分布直方图知不健康生活方式者概率为0.2,超健康生活方式者的概率为0.1,一般生活方式者的概率为0.7,0≤X≤60,X的可能取值为0,10,20,30,40,50,60,利用相互独立与互斥事件的概率计算公式即可得出.
【考点精析】解答此题的关键在于理解频率分布直方图的相关知识,掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息,以及对离散型随机变量及其分布列的理解,了解在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.

 阅读快车系列答案
阅读快车系列答案【题目】某医疗科研项目对5只实验小白鼠体内的A、B两项指标数据进行收集和分析,得到的数据如下表:
指标 | 1号小白鼠 | 2号小白鼠 | 3号小白鼠 | 4号小白鼠 | 5号小白鼠 |
A | 5 | 7 | 6 | 9 | 8 |
B | 2 | 2 | 3 | 4 | 4 |
(1)若通过数据分析,得知A项指标数据与B项指标数据具有线性相关关系,试根据上表,求B项指标数据y关于A项指标数据x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() ;
;
(2)现要从这5只小白鼠中随机抽取3只,求其中至少有一只B项指标数据高于3的概率. 参考公式: ![]() =
= 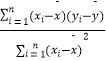 =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.
【题目】某公司有A、B、C、D、E五辆汽车,其中A、B两辆汽车的车牌尾号均为1,C、D两辆汽车的车牌尾号均为2,E车的车牌尾号为6.已知在非限行日,每辆车可能出车或不出车,A、B、E三辆汽车每天出车的概率均为 ![]() ,C、D两辆汽车每天出车的概率均为
,C、D两辆汽车每天出车的概率均为 ![]() ,五辆汽车是否出车相互独立,该公司所在地区汽车限行规定如下:
,五辆汽车是否出车相互独立,该公司所在地区汽车限行规定如下:
工作日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
限行车牌尾号 | 0和5 | 1和6 | 2和7 | 3和8 | 4和9 |
例如,星期一禁止车牌尾号为0和5的车辆通行.
(1)求该公司在星期一至少有2辆汽车出车的概率;
(2)设X表示该公司在星期二和星期三两天出车的车辆数之和,求X的分布列及数学期望.