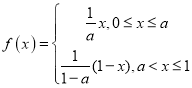题目内容
【题目】已知关于![]() 的不等式
的不等式![]() ,其中
,其中![]() ;
;
(1)试求不等式的解集![]() ;
;
(2)对于不等式的解集![]() ,记
,记![]() (其中
(其中![]() 为整数集),若集合
为整数集),若集合![]() 为有限集,求实数
为有限集,求实数![]() 的取值范围,使得集合
的取值范围,使得集合![]() 中元素个数最少,并用列举法表示集合
中元素个数最少,并用列举法表示集合![]() ;
;
【答案】(1)答案见解析 (2)![]() ,
,![]()
【解析】
(1)对![]() 进行分类讨论,分别讨论
进行分类讨论,分别讨论![]() ,
,![]() ,
,![]() 或
或![]() ,
,![]() 的情况,进而求解即可;
的情况,进而求解即可;
(2)由(1)可知当![]() 时,集合
时,集合![]() 为有限集,利用对勾函数可知
为有限集,利用对勾函数可知![]() ,当且仅当
,当且仅当![]() 时等号成立,进而求解即可
时等号成立,进而求解即可
(1)当![]() ,
,![]() ;
;
当![]() 时,令
时,令![]() ,解得
,解得![]() 或
或![]() ,
,
则当![]() 或
或![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
①当![]() ,
,![]() ;
;
②当![]() 或
或![]() ,
,![]() 或
或![]() ;
;
③当![]() ,
,![]() 或
或![]() ;
;
(2)因为![]() (其中
(其中![]() 为整数集),
为整数集),
由(1),当![]() 时,集合
时,集合![]() 中的元素的个数无限;
中的元素的个数无限;
当![]() 时,集合
时,集合![]() 中的元素的个数有限,此时集合
中的元素的个数有限,此时集合![]() 为有限集,
为有限集,
因为![]() ,所以
,所以![]() ,当且仅当
,当且仅当![]() ,即
,即![]() 时等号成立,
时等号成立,
所以当![]() 时,集合
时,集合![]() 的元素个数最少,此时
的元素个数最少,此时![]() ,
,
所以![]()

练习册系列答案
相关题目