题目内容
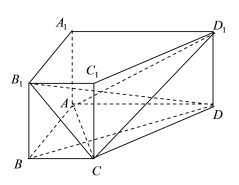
【题目】已知正方体
的棱长为4，E、F分别是棱AB、
的中点，联结EF、
、
、
E、
E、
E.
求三棱锥
的体积；
求直线
与平面
所成角的大小
结果用反三角函数值表示
．
【答案】（1）
；（2）
【解析】
先由题意连结EF、
、
、
E、
E、
E，根据三棱锥的体积公式可得
进而可求出结果；
以D为原点，DA，DC，
所在直线分别为x，y，z轴，建立空间直角坐标系，求出直线
的方向向量和平面
的法向量，根据两向量夹角的余弦值即可求出结果.
正方体
的棱长为4，E、F分别是棱AB、
的中点，
连结EF、、、E、E、E.
三棱锥
的体积
．
以D为原点，DA，DC，所在直线分别为x，y，z轴，建立空间直角坐标系，
0，
，
2，
，
4，，
2，，
2，，
0，，
，
设平面的法向量
y，
，
则
，取
，得
，
设直线与平面所成角的大小为
，
则
，
直线与平面所成角的大小为．
练习册系列答案
相关题目
【题目】某企业生产甲、乙两种产品均需要
，
两种原料，已知生产1吨每种产品所需原料及每天原料的可用限额如表所示．如果生产1吨甲、乙产品可获得利润分别为3万元、4万元，则该企业每天可获得最大利润为（ ）
甲 | 乙 | 原料限额 | |
| 3 | 2 | 10 |
| 1 | 2 | 6 |
A. 10万元B. 12万元C. 13万元D. 14万元
