题目内容
【题目】如图,在四棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,且
,且![]() .
.
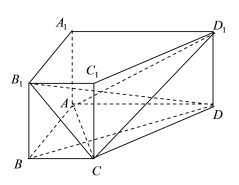
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ) 求证:![]() ;
;
(Ⅲ) 若 ![]() ,判断直线
,判断直线![]() 与平面
与平面 ![]() 是否垂直?并说明理由.
是否垂直?并说明理由.
【答案】(Ⅰ)见解析; (Ⅱ)见解析; (Ⅲ)见解析.
【解析】
(Ⅰ)由题意结合几何关系可证得平面BCC1B1∥平面ADD1A1,据此结合面面平行的性质即可证得题中的结论;
(Ⅱ)由题意可证得AC⊥平面BB1D,据此证明题中的结论即可;
(Ⅲ)结论:直线B1D与平面ACD1不垂直,利用反证法,假设B1D⊥平面ACD1,结合题意得到矛盾的结论即可说明直线B1D与平面ACD1不垂直.
证明:(Ⅰ)∵AD∥BC,BC平面ADD1A1,AD平面ADD1A1,
∴BC∥平面ADD1A1,
∵CC1∥DD1,CC1平面ADD1A1,DD1平面ADD1A1,
∴CC1∥平面ADD1A1,
又∵BC∩CC1=C,
∴平面BCC1B1∥平面ADD1A1,
又∵B1C平面BCC1B1,
∴B1C∥平面ADD1A1.
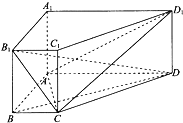
(Ⅱ)∵BB1⊥平面ABCD,AC底面ABCD,∴BB1⊥AC,又∵AC⊥BD,BB1∩BD=B,
∴AC⊥平面BB1D,
又∵B1D底面BB1D,
∴AC⊥B1D;
(Ⅲ)结论:直线B1D与平面ACD1不垂直,
证明:假设B1D⊥平面ACD1,
由AD1平面ACD1,可得B1D⊥AD1,
由棱柱![]() 中,BB1⊥底面ABCD,∠BAD=90°,
中,BB1⊥底面ABCD,∠BAD=90°,
可得:A1B1⊥AA1,A1B1⊥A1D1,
又∵AA1∩A1D1=A1,
∴A1B1⊥平面AA1D1D,
∴A1B1⊥AD1,
又∵A1B1∩B1D=B1,
∴AD1⊥平面A1B1D,
∴AD1⊥A1D,
这与四边形AA1D1D为矩形,且AD=2AA1矛盾,故直线B1D与平面ACD1不垂直.

练习册系列答案
相关题目

